题目内容
如图，一张矩形ABCD卡片放在每格宽度为6mm的横格纸中，恰好四个顶点都在横格线上，已知∠α=36°，求矩形ABCD卡片的周长．（精确到1mm，参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）分析：作BE⊥l于点E，DF⊥l于点F，求∠ADF的度数，在Rt△ABE中，可以求得AB的值，在Rt△ADF中，可以求得AD的值，即可计算矩形ABCD的周长，即可解题．
解答：
解：作BE⊥l于点E，DF⊥l于点F．
∵α+∠DAF=180°-∠BAD=180°-90°=90°，
∠ADF+∠DAF=90°，
∴∠ADF=α=36°．
根据题意，得BE=12mm，DF=24mm．
在Rt△ABE中，sin α=
，
∴AB=
=
=20mm
在Rt△ADF中，cos∠ADF=
，
∴AD=
=
=30m．
∴矩形ABCD的周长=2×（20+30）=100mm．
答：矩形ABCD卡片的周长是100mm．
解：作BE⊥l于点E，DF⊥l于点F．∵α+∠DAF=180°-∠BAD=180°-90°=90°，
∠ADF+∠DAF=90°，
∴∠ADF=α=36°．
根据题意，得BE=12mm，DF=24mm．
在Rt△ABE中，sin α=
| BE |
| AB |
∴AB=
| BE |
| sin36° |
| 12 |
| 0.60 |
在Rt△ADF中，cos∠ADF=
| DF |
| AD |
∴AD=
| DF |
| cos36° |
| 24 |
| 0.80 |
∴矩形ABCD的周长=2×（20+30）=100mm．
答：矩形ABCD卡片的周长是100mm．
点评：本题考查了矩形对边相等的性质，直角三角形中三角函数的应用，锐角三角函数值的计算．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
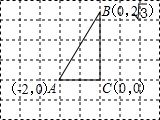BC的2倍，“宝藏”就在矩形未知的顶点处，那么“宝藏”的位置可能是
10、如图是一张矩形纸片ABCD，AB=10，AD=4，若用剪刀沿∠ABC的角平分线BE剪下，则DE的长等于（ ）
如图是一张矩形纸片ABCD，AB=10，AD=4，若用剪刀沿∠ABC的角平分线BE剪下，则DE的长等于