题目内容
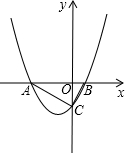如图，抛物线y=ax2+2ax+c（a＞0）与y轴交于点C，与x轴交于A、B两点，A点在B点左侧．若点E在x轴上，点P在抛物线上，且以A、C、E、P为顶点的四边形是平行四边形，则符合条件的点P有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析：由于以A、C、E、P为顶点的平行四边形并没有明确边和对角线，所以要分两种情况讨论：
①以AC为边，那么EP∥AC，且EP=AC；
②以AC为对角线，那么AE必与CP平行，因此CP∥x轴；
根据上述两种情况，通过画图可找出符合条件的点P的个数．
解答：①以AC为边时，EP
AC，共两种情况，如图①；
②以AC为对角线时，AE∥CP，由于点E在x轴上，因此CP∥x轴，过点C作x轴的平行线，与抛物线的交点也符合点P的条件，如图②；
综上，共有三个符合条件的P点，故选C．
点评：在不明确平行四边形四顶点的排序顺序时，一定需要进行分类讨论，由于题目是选择题，因此只需根据平行四边形的特点，通过作图找出符合条件的P点的个数即可．
分析：由于以A、C、E、P为顶点的平行四边形并没有明确边和对角线，所以要分两种情况讨论：
①以AC为边，那么EP∥AC，且EP=AC；
②以AC为对角线，那么AE必与CP平行，因此CP∥x轴；
根据上述两种情况，通过画图可找出符合条件的点P的个数．
解答：①以AC为边时，EP
AC，共两种情况，如图①；②以AC为对角线时，AE∥CP，由于点E在x轴上，因此CP∥x轴，过点C作x轴的平行线，与抛物线的交点也符合点P的条件，如图②；
综上，共有三个符合条件的P点，故选C．
点评：在不明确平行四边形四顶点的排序顺序时，一定需要进行分类讨论，由于题目是选择题，因此只需根据平行四边形的特点，通过作图找出符合条件的P点的个数即可．
练习册系列答案
相关题目
两点，试问当x为何值时，线段CD有最大值，其最大值为多少？
O为坐标原点，抛物线上一点C的横坐标为1．
此抛物线上，矩形面积为12，
与x轴交于点A、B，点A的坐标为（-2，0）．