题目内容
已知,直角三角形ABC中,∠C=90°,点D、E分别是边AC、AB的中点,BC=6.
(1)如图1,动点P从点E出发,沿直线DE方向向右运动,则当EP=______时,四边形BCDP是矩形;
(2)将点B绕点E逆时针旋转.
①如图2,旋转到点F处,连接AF、BF、EF.设∠BEF=α°,求证:△ABF是直角三角形;
②如图3,旋转到点G处,连接DG、EG.已知∠BEG=90°,求△DEG的面积.

图1 图2 图3
(1)3;………………1分
(2)
①∵点E是边AB的中点,∴AE=BE.
由题意可得,BE=EF.∴BE=EF=AE.………………2分
在△BEF中,∠BEF=α°,可得∠EBF=∠BFE=90°-![]() α°.
α°.
在△AEF中,可得∠EAF=∠AFE=![]() α°.………………4分
α°.………………4分
∴∠BFE+∠AFE =90°-![]() α°+
α°+![]() α°=90°.
α°=90°.
∴△ABF是直角三角形;………………5分
②解法一 如图4,将点D绕点E顺时针旋转90°,到达点H,连接EH、BH.
 |
图4 图5 图6
可证明△DEG≌△HEB.………………7分
求得△HEB的面积为![]() ,∴△DEG的面积为
,∴△DEG的面积为![]() .………………9分
.………………9分
解法二 如图5,过点E作边BC的垂线,垂足为点K,过点G作直线EK的垂线,垂足为点H.
可证明△EHG≌△BKE.………………7分
∴EH=BK=3.
∴△DEG的面积为![]() .………………9分
.………………9分
解法三 如图6,过点E作边BC的垂线,垂足为点K,过点G作直线DE的垂线,垂足为点M.
可证明△GME≌△BKE.………………7分
∴GM=BK=3.
∴△DEG的面积为![]() .………………9分
.………………9分

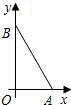 已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.