题目内容
武汉二中科学兴趣小组的同学把一种珍贵药用植物分别放在不同的环境中，经过一定时间后，测试出这种植物高度的增长情况（如表）．
| 温度t/℃ | -6 | -4 | 2 | 0 | 2 | 4 | 6 |
| 植物高度增长量（mm） | … | … | 49 | 49 | 41 | … | … |
（1）求出y与t之间的函数关系．
（2）求这种植物高度最大可以增长多少mm？
（3）若该种植物的增长高度在14～25mm之间药用价值最为理想，问应如何控制植物适合生长的温度．
解：（1）y=at2+bt+c，
将点（-2，49）、（0，49），（2，41）代入可得：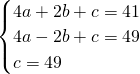
，
解得：
．
故y=-t2-2t+49．
（2）由（1）得，y=-（t+1）2+50，
当t=1°C时，这种植物高度增长最大，最大可以增长50mm；
（3）由题意得，14＜y＜25mm，即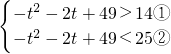
，
解①得：-7＜t＜5；
解②得：t＞4或t＜-6；
综上可得：4＜t＜5或-7＜t＜-6．
答：该种植物的增长高度在14～25mm之间药用价值最为理想，应控制植物生长的温度在4°C至5°C 或-7°C至-6°C之间．
分析：（1）设y=at2+bt+c，选择三点代入即可得出a、b、c的值，继而得出y与t之间的函数关系．
（2）利用配方法求最值即可；
（3）根据题意得出不等式，解出即可．
点评：本题考查了二次函数的应用，解答本题的关键是结合表格信息求出二次函数关系式，注意掌握配方法求二次函数最值的应用．
将点（-2，49）、（0，49），（2，41）代入可得：
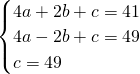，解得：
．故y=-t2-2t+49．
（2）由（1）得，y=-（t+1）2+50，
当t=1°C时，这种植物高度增长最大，最大可以增长50mm；
（3）由题意得，14＜y＜25mm，即
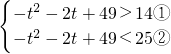，解①得：-7＜t＜5；
解②得：t＞4或t＜-6；
综上可得：4＜t＜5或-7＜t＜-6．
答：该种植物的增长高度在14～25mm之间药用价值最为理想，应控制植物生长的温度在4°C至5°C 或-7°C至-6°C之间．
分析：（1）设y=at2+bt+c，选择三点代入即可得出a、b、c的值，继而得出y与t之间的函数关系．
（2）利用配方法求最值即可；
（3）根据题意得出不等式，解出即可．
点评：本题考查了二次函数的应用，解答本题的关键是结合表格信息求出二次函数关系式，注意掌握配方法求二次函数最值的应用．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目