题目内容
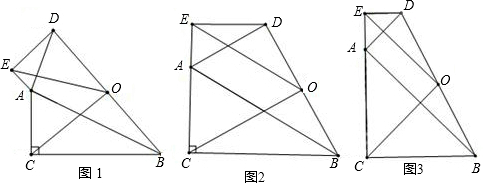
已知：如图①所示，在
和
中，
，
，
，且点
在一条直线上，连接
分别为
的中点．
（1）求证：
；
（2）求证：
是等腰三角形；
（3）在图①的基础上，将绕点
按顺时针方向旋转，使D点落在线段AB上，其他条件不变，得到图②所示的图形．（1）、（2）中的两个结论是否仍然成立吗？请你直接写出你的结论．
【答案】
（1）证明：
．
∴
，即
．
，
．
．
．
（2）证明：由(1)得
,∴
，
．
分别是
的中点，
．
又．
．
，即
为等腰三角形．
（3）（1）、（2）中的两个结论仍然成立．
【解析】（1）由题中条件可得△ABE≌△ACD，进而可得BE=CD；
（2）有（1）中△ABE≌△ACD，可得对应边、对应角相等，进而得出△ABM≌△ACN，即可得出结论；
（3）旋转之后，由题中条件仍可得出△ABE≌△ACD，△ABE≌△ACD，所以（1）、（2）中结论仍成立．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
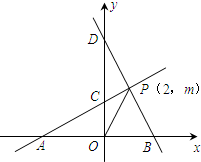已知，如图1所示，直线PA与x轴交于点A，与y轴交于点C（0，2），且S△AOC=4，直线BD与x轴交于点B，与y轴交于点D，直线PA与直线BD交于点P（2，m），点P在第一象限，连接OP．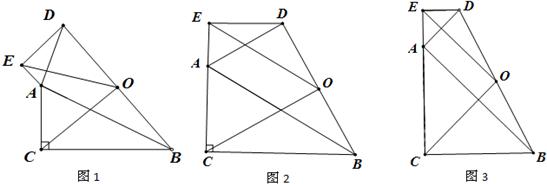
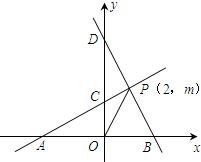已知，如图1所示，直线PA与x轴交于点A，与y轴交于点C（0，2），且S△AOC=4，直线BD与x轴交于点B，与y轴交于点D，直线PA与直线BD交于点P（2，m），点P在第一象限，连接OP．
