Question

【题目】如图，已知函数的图象与一次函数的图象相交不同的点A、B，过点A作AD⊥轴于点D，连接AO，其中点A的横坐标为，△AOD的面积为2.

(1)求的值及=4时的值；

(2)记表示为不超过的最大整数，例如：，，设,若，求值

Answer 1

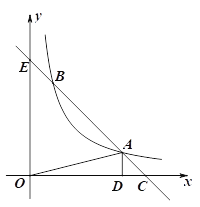
【答案】（1）4；1；（2）5.

【解析】（1）设A（x0，y0），可表示出△AOD的面积，再结合x0y0=k可求得k的值，根据A的横坐标可得纵坐标，代入一次函数可得m的值；

（2）先根据一次函数与x轴的交点确定OC的长，表示DC的长，从而可以表示t，根据A的横坐标为x0，即x0满足＝mx+5，可得：mx02+5x0=4，再根据m的取值计算m2t，最后利用新定义可得结论．

（1）设A（x0，y0），则OD=x0，AD=y0，

∴S△AOD=ODAD=x0y0=2，

∴k=x0y0=4；

当x0=4时，y0=1，

∴A（4，1），

代入y=mx+5中得4m+5=1，m=-1；

（2）∵，

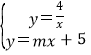∴＝mx+5，整理得，mx2+5x-4=0，

∵A的横坐标为x0，

∴mx02+5x0=4，

当y=0时，mx+5=0，

x=-，

∵OC=-，OD=x0，

∴m2t=m2（ODDC），

=m2x0（--x0），

=m（-5x0-mx02），

=-4m，

∵-＜m＜-，

∴5＜-4m＜6，

∴[m2t]=5．