Question

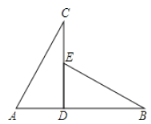
【题目】已知：如图，AB是⊙O的直径，弦CD⊥AB于点E，G是上一动点，AG，DC的延长线交于点F，连结BC．

（1）若AB=4，∠B=60°，求的长；

（2）设∠DGF=°，∠BCD=°，求关于的函数表达式．

Answer 1

【答案】（1）；（2）=+90．

【解析】

（1）根据垂径定理可得的度数是120°．根据弧长 公式可得；（2）连结AC，则∠ACD=∠AGD=180°-∠DGF=(180-)°．由直径所对圆周角是直角可得∠ACD+∠BCD=90°．所以，(180-)+=90，整理可得.

解：（1）∵∠AGD=60°，直径AB⊥CD，

∴∠BCD=90°-60°=30°,

∴=60°，

∴=120°．

∵r=AB=2，

∴ ．

（2）连结AC，则∠ACD=∠AGD=180°-∠DGF=(180-)°．

∵AB是直径，

∴∠ACB=90°，即∠ACD+∠BCD=90°．

∵∠BCD=°，

∴(180-)+=90，

∴=+90．