题目内容
二次函数y=ax2+bx+c的图象与x轴的两个不同的交点为A、B,抛物线顶点为C.则S△ABC=________.

分析:根据二次函数y=ax2+bx+c的图象与x轴的两个不同的交点,得出b2-4ac≥0,求出当y=0时,x的值,即可求出AB,再求出抛物线顶点C的纵坐标,根据三角形的面积公式即可求出答案.
解答:∵二次函数y=ax2+bx+c的图象与x轴的两个不同的交点,
∴b2-4ac≥0,
当y=0时,ax2+bx+c=0,
解得:x1=
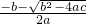 ,x2=
,x2=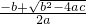 ,
,∴AB=|
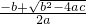 -
-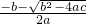 |=
|=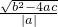 ,
,抛物线顶点C的纵坐标是
 ,
,∴S△ABC=
 ×
×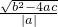 ×|
×| |=
|= .
.故答案为:
 .
.点评:本题主要考查对抛物线与X轴的交点,根的判别式,三角形的面积,用公式法解一元二次方程等知识点的理解和掌握,此题是一个拔高的题目,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 点C
点C 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是
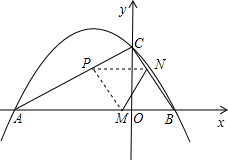
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是 (2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:
(2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法: