题目内容
如图在△ABC中，D、E分别为AB、AC上的点，且BD＝CE，M、N分别是BE、CD的中点．过MN的直线交AB于P，交AC于Q，线段AP、AQ相等吗?为什么?
找到BC的中点H，连接MH，NH．如图：
∵M，H为BE，BC的中点，∴MH∥EC，且MH=
EC．
∵N，H为CD，BC的中点，∴NH∥BD，且NH=BD．
∵BD=CE，∴MH=NH．∴∠HMN=∠HNM；（3分）
∵MH∥EC，∴∠HMN=∠PQA，
同理∠HNM=∠QPA．
∴△APQ为等腰三角形，
∴AP=AQ．（6分）
解析:根据中位线定理证明MH=NH，进而证明∠HMN=∠HNM，∠HMN=∠PQA，所以△APQ为等腰三角形，即AP=AQ．
练习册系列答案
考前必练系列答案
相关题目
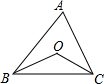如图在△ABC中，∠ABC=50°，∠ACB=75°，点O是内心，则∠BOC的度数为
如图在△ABC中，∠A=45°，tanB=3，BC=
已知，如图在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG平分∠CDE，DC=AE，
如图在△ABC中，AD垂直平分BC，AD=8，BC=10，E、F是AD上的两点，则图中阴影部分的面积是