题目内容
如图,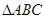 中,
中,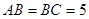 ,
,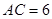 ,过点
,过点 作
作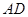 ∥
∥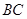 ,点
,点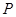 、
、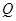 分别是射线
分别是射线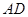 、线段
、线段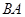 上的动点,且
上的动点,且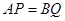 ,过点
,过点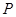 作
作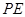 ∥
∥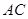 交线段
交线段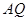 于点
于点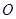 ,联接
,联接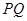 ,设
,设 面积为
面积为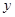 ,
,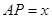 .
.

(1)用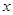 的代数式表示
的代数式表示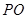 ;
;
(2)求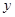 与
与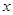 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接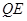 ,若
,若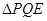 与
与 相似,求
相似,求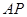 的长.
的长.
(1) (2)
(2) (3)
(3)
【解析】
试题分析:(1)∵ ∥
∥ ,
, ∥
∥ ,
,
∴四边形 是平行四边形
是平行四边形
∴ ,
,
 ,
,
可得
(2)∵ ,
,
∴∠ ∠
∠
又∠ =∠
=∠ ,∠
,∠ =∠
=∠ ,
,
∴∠ =∠
=∠ ,
,
∴
∴当 时,
时, ;
;
作 ,
, ,垂足分别为点
,垂足分别为点 、
、 ,
,

则易得 ,
, ,
, ,
,
由∠ =∠
=∠ ,∠
,∠ =∠
=∠
得△ ∽△
∽△
∴ ,
,
∴ ,
,
∴

所以 与
与 的函数关系式是
的函数关系式是

(3)【解法一】当 时
时
由 ,
, ,∠
,∠ ∠
∠
可得△ ≌△
≌△ ,于是
,于是
由于∠ ∠
∠ ,
,
所以若△ 与△
与△ 相似,
相似,
只有△ ∽△
∽△
可得
于是得 ,解得
,解得
同理当 ,可得
,可得 (不合题意,舍去)
(不合题意,舍去)
所以,若△ 与△POQ相似,AP的长为
与△POQ相似,AP的长为 。
。
【解法二】当 时,可得
时,可得 ,
,
于是得 ,
,

由于∠ =∠
=∠ ,
,
所以若△ 与△
与△ 相似,只有△
相似,只有△ ∽△
∽△


解得 ,
, (不合题意,舍去)
(不合题意,舍去)
所以,若△ 与△
与△ 相似,
相似, 的长为
的长为
考点:函数和相似三角形
点评:本题考查求函数的关系式和相似三角形的证明,要求考生会求函数的关系式,以及相似三角形的证明方法

 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案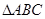 中,
中,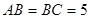 ,
,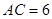 ,过点
,过点 作
作 ∥
∥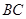 ,点
,点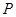 、
、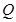 分别是射线
分别是射线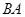 上的动点,且
上的动点,且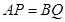 ,过点
,过点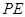 ∥
∥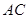 交线段
交线段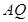 于点
于点 ,联接
,联接 ,设
,设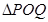 面积为
面积为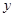 ,
, .
.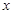 的代数式表示
的代数式表示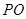 ;
;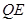 ,若
,若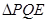 与
与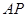 的长.
的长.
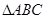 中,
中, ,
,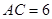 ,过点
,过点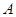 作
作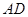 ∥
∥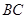 ,点
,点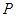 、
、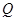 分别是射线
分别是射线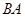 上的动点,且
上的动点,且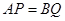 ,过点
,过点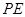 ∥
∥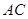 交线段
交线段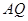 于点
于点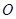 ,联接
,联接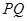 ,设
,设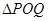 面积为
面积为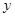 ,
,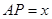 .
.
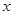 的代数式表示
的代数式表示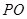 ;
;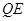 ,若
,若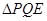 与
与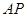 的长.
的长.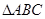 中,
中,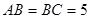 ,
,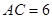 ,过点
,过点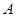 作
作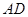 ∥
∥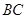 ,点
,点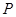 、
、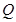 分别是射线
分别是射线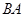 上的动点,且
上的动点,且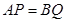 ,过点
,过点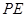 ∥
∥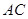 交线段
交线段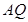 于点
于点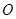 ,联接
,联接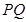 ,设
,设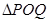 面积为
面积为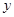 ,
,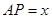 .
.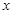 的代数式表示
的代数式表示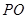 ;
;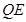 ,若
,若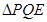 与
与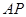 的长.
的长.
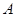 为圆心,
为圆心,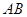 为半径作圆
为半径作圆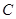 (如图(1)),过点
(如图(1)),过点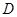 ,以点
,以点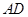 为半径作圆交网格于点
为半径作圆交网格于点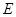
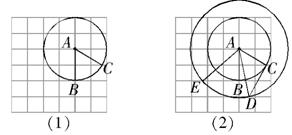
 问题:
问题: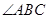 的度数;
的度数;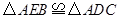 ;
;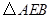 可以看作是由
可以看作是由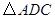 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断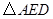 的形状(不用说明理由).
的形状(不用说明理由).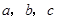 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形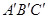 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线