Question

在底角等于80°的等腰△ABC的两腰AB、AC上，分别取点D、E，使得∠BDC=50°，∠BEC=40°．则∠ADE=

50°

．

Answer 1

分析：在CE上取一点F，使∠CBF=20°，连接BF，DF，根据三角形内角和定理及等腰三角形的性质可求得∠BAC的度数，再根据三角形内角和定理可求得，∠CBE，∠ABE，∠EBF的订数，从而可得到BF=EF，进而可推出BC=BF，从而可判定△BDF为等边三角形，根据等边三角形的性质可推出∠DFE与∠FED的度数，从而不难求解．

解答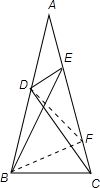：解：在CE上取一点F，使∠CBF=20°，连接BF，DF．
∵∠ABC=∠ACB=80°，
∴∠BAC=20°，
∵∠BDC=50°，
∴BC=BD，∠CBE=60°，∠ABE=20°，∠EBF=40°，
∴BF=EF，∠DBF=60°，
∴∠BFC=80°，
∴BC=BF，
∴△BDF为等边三角形，
∴BF=DF，
∴DF=EF，
∵∠BFD=60°，
∴∠DFE=40°，
∴∠FED=70°
∴∠ADE=50°，
故答案为：50°．

点评：此题主要考查等腰三角形的性质，三角形内角和定理及等边三角形的判定与性质的综合运用．