题目内容
(2002•广元)在数学活动课中,测量组为了测量河对岸高层建筑物AB的高度,在C处用测角仪由点D测得顶端A的仰角是30°,向高层建筑前进30米到达C'处,由D'测得顶端A的仰角为45°,已知测量仪高1.1米,求建筑物AB的高.( ≈1.732结果保留2个有效数字)
≈1.732结果保留2个有效数字)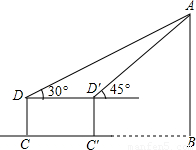
【答案】分析:延长DD′交AB于E,易知DE⊥AB;在Rt△AD′E中,可设AE=x,利用已知角的三角函数可用x表示出D′E的长,进而可表示出DE的长;在Rt△ADE中,根据仰角∠ADE的正切函数即可列方程求出AE的长.
解答: 解:延长DD′交AB于E,则DE⊥AB;
解:延长DD′交AB于E,则DE⊥AB;
设AE=xm,在Rt△AD′E中,∠AD′E=45°,
∴D′E=AE=xm;
在Rt△AED中,∠ADE=30°,AE=x,DE=30+x,
则tan30°= ,即
,即 ;
;
解得:x=15 +15;
+15;
∴AB=AE+BE=15×1.732+1.1≈27(米);
答:建筑物AB的高约为27米.
点评:本题考查直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.
解答:
 解:延长DD′交AB于E,则DE⊥AB;
解:延长DD′交AB于E,则DE⊥AB;设AE=xm,在Rt△AD′E中,∠AD′E=45°,
∴D′E=AE=xm;
在Rt△AED中,∠ADE=30°,AE=x,DE=30+x,
则tan30°=
 ,即
,即 ;
;解得:x=15
 +15;
+15;∴AB=AE+BE=15×1.732+1.1≈27(米);
答:建筑物AB的高约为27米.
点评:本题考查直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.

练习册系列答案
相关题目
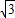 ≈1.732结果保留2个有效数字)
≈1.732结果保留2个有效数字)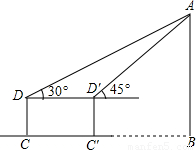

 都经过A点关于x轴的对称点A',试求m、n的值,并求直线与双曲线的另一个交点的坐标.
都经过A点关于x轴的对称点A',试求m、n的值,并求直线与双曲线的另一个交点的坐标.