Question

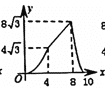
【题目】如图，抛物线交轴于点和点，交轴于点．

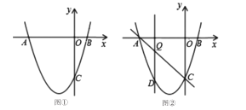
（1）求抛物线的函数表达式；

（2）若点在抛物线上，且，求点的坐标；

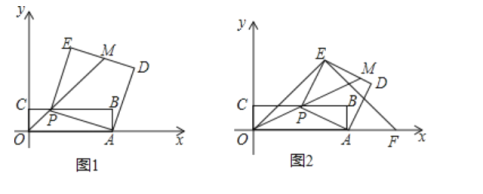
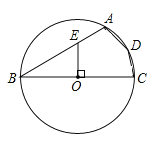
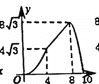
（3）如图②，设点是线段上的一动点，作轴，交抛物线于点，是否存在面积的最大值？若存在，请求出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）点的坐标为或或或；（3）

【解析】

（1）把点A、C的坐标分别代入函数解析式，列出关于系数的方程组，通过解方程组求得系数的值；
（2）设P点纵坐标为，根据列出关于m的方程，解方程求出m的值，进而得到点P的坐标；
（3）先运用待定系数法求出直线AC的解析式为y＝-x-4，再设Q点坐标为（t，-t-4），则D点坐标为（t，t+3t-4），然后用含t的代数式表示QD，根据二次函数的性质即可求出线段QD长度的最大值．

解：（1）∵抛物线交轴于点和点，交轴于点，

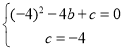∴ ，解得 ，

∴；

（2）设点的纵坐标为

∵

∴，

∴，

∴或

解得：或2或或

∴点的坐标为或或或

（3）存在．

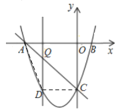
设AC解析式为，待入A，C点坐标，

，解得，

∴AC解析式为，

∵点在线段上

∴点的坐标为

∵轴，交抛物线于点，

∴点的坐标为

∴

∴当时，的值最大．

又∵

∴的值最大时，的面积最大．

∴