题目内容
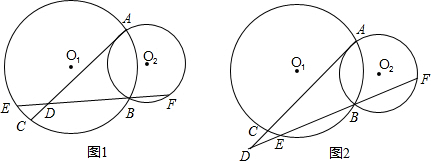
 已知:⊙O1与⊙O2外切于P,AC是过P点的割线,交⊙O1于A,交⊙O2于C,BC切⊙O2于C,过点O1作直线AB交BC于B.求证:AB⊥BC.
已知:⊙O1与⊙O2外切于P,AC是过P点的割线,交⊙O1于A,交⊙O2于C,BC切⊙O2于C,过点O1作直线AB交BC于B.求证:AB⊥BC.
 解:连接O1O2,O2C,
解:连接O1O2,O2C,∵BC切⊙O2于C,
∴O2C⊥BC,
∵O1O2连接线经过P,
∴AO1=O1P,O2P=O2C,
又∵∠O1PA=∠O2PC,
∴∠PAO1=∠O1PA=∠O2PC=∠O2CP,
∴AB∥O2C,
∴AB⊥BC.
分析:利用相切两圆的性质得出O1O2连接线经过P,进而得出∠PAO1=∠O1PA=∠O2PC=∠O2CP,即可得出AB∥O2C,求出即可.
点评:此题主要考查了相切两圆的性质以及切线的性质,根据已知得出∠PAO1=∠O1PA=∠O2PC=∠O2CP是解题关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.
11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.