题目内容
已知平面内有n(n≥3,且n为整数)个点,其中无任何三点在同一条直线上.过其中任意两点画线段,可得an条线段;以其中任意三点为顶点画三角形,可得bn个三角形.

(1)请你依照题意,在图③、图④中完成作图;
(2)观察图形,完成下表:
(3)照此规律,an=
;bn-bn-1=
.

(1)请你依照题意,在图③、图④中完成作图;
(2)观察图形,完成下表:
| n | 3 | 4 | 5 | 6 |
| 示意图 | 图① | 图② | 图③ | 图④ |
| an | 3 | 6 | ||
| bn | 1 | 4 |
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| (n-1)(n-2) |
| 2 |
| (n-1)(n-2) |
| 2 |
分析:(1)顺次连接所有的点即可得到正确的图形;
(2)所有线段是多边形的边数加上多边形的对角线的条数;
(3)根据上题总结的规律填写即可.
(2)所有线段是多边形的边数加上多边形的对角线的条数;
(3)根据上题总结的规律填写即可.
解答:解:(1)根据题意是顺次连接所有的点得到多边形,如图:

(2)如下表:
(3)平面上有n个点,每个点和除自身外的n-1个点可以连线,但每条线都重复两次,故an=
;
平面上有n个点,过不在同一条直线上的三个点可以确定一个三角形,取第一个点A有n种方法,取第二个点有B有(n-1)种取法,取第三个点C有(n-2)种取法,
所以一共可以作n(n-1)(n-2)个三角形,但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形,
故应除以6,
即bn=
,
∴bn-bn-1=
-
=
.

(2)如下表:
| n | 3 | 4 | 5 | 6 |
| 示意图 | 图① | 图② | 图③ | 图④ |
| an | 3 | 6 | 10 | 15 |
| bn | 1 | 4 | 10 | 20 |
| n(n-1) |
| 2 |
平面上有n个点,过不在同一条直线上的三个点可以确定一个三角形,取第一个点A有n种方法,取第二个点有B有(n-1)种取法,取第三个点C有(n-2)种取法,
所以一共可以作n(n-1)(n-2)个三角形,但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形,
故应除以6,
即bn=
| n(n-1)(n-2) |
| 6 |
∴bn-bn-1=
| n(n-1)(n-2) |
| 6 |
| (n-1)(n-2)(n-3) |
| 6 |
| (n-1)(n-2) |
| 2 |
点评:本题考查了规律型:图形的变化,是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
相关题目
已知平面内有一点P,它的横坐标与纵坐标互为相反数,且与原点的距离是2,则P点的坐标为( )
| A、(-1,1)或(1,-1) | ||||||||
| B、(1,-1) | ||||||||
C、(-
| ||||||||
D、(
|
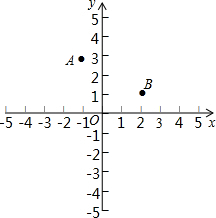 已知平面内有两点A(-1,3)、B(2,1),x轴上有一点P满足PA+PB的值最小,请在x轴上标出点P的位置,并求出点P的坐标.
已知平面内有两点A(-1,3)、B(2,1),x轴上有一点P满足PA+PB的值最小,请在x轴上标出点P的位置,并求出点P的坐标.