Question

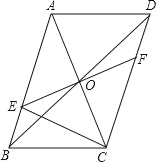
【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，EF过点O且与AB、CD分别相交于点E、F，连接EC．

（1）求证：OE=OF；

（2）若EF⊥AC，平行四边形ABCD的周长是22，求△BEC的周长．

Answer 1

【答案】（1）见解析；（2）11.

【解析】

（1）由已知条件证△DFO≌△BEO即可得到结论；

（2）由平行四边形ABCD的周长为22可得AB+BC=11；由已知易得点O是AC的中点，结合EF⊥AC可得EF是AC的垂直平分线，由此可得AE=EC，从而可得△BEC的周长=BC+BE+EC=BC+BE+AE=BC+AB=11.

（1）∵四边形ABCD是平行四边形，

∴OD=OB，DC∥AB，

∴∠FDO=∠EBO，

在△DFO和△BEO中，

∠FDO=∠EBO，OD=OB，∠FOD=∠EOB，

∴△DFO≌△BEO（ASA），

∴OE=OF．

（2）∵四边形ABCD是平行四边形，

∴AB＝CD，AD＝BC，OA＝OC.

∵EF⊥AC，

∴AE＝CE.

∵平行四边形ABCD的周长是22，即2(BC＋AB)＝22.

∴BC＋AB=11，

∴△BEC的周长=BC＋BE＋CE＝BC＋BE＋AE＝BC＋AB＝11.