题目内容
(本题满分12分)在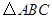 中,
中,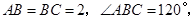 将
将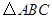 绕点
绕点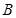 顺时针旋转角
顺时针旋转角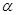
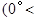
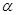
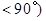 得
得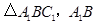 交
交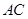 于点
于点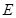 ,
,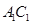 分别交
分别交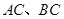 于
于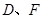 两点.
两点.
1.(1)如图1,观察并猜想,在旋转过程中,线段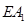 与
与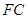 有怎样的数量关系?并证明你的结论;
有怎样的数量关系?并证明你的结论;
2.(2)如图2,当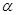
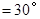 时,试判断四边形
时,试判断四边形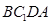 的形状,并说明理由;
的形状,并说明理由;
3.(3)在(2)的情况下,求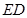 的长.
的长.
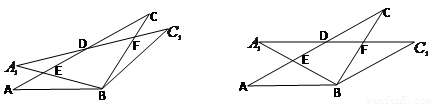
【答案】
1.(1)
证明:(证法一)
由旋转可知,
∴
∴ 又
又
∴ 即
即
(证法二)
由旋转可知, 而
而
∴
∴ ∴
∴
即 -
-
2.(2)四边形 是菱形.
是菱形.
证明: 同理
同理
∴四边形 是平行四边形.
是平行四边形.
 又
又 ∴四边形
∴四边形 是菱形
是菱形
3.(3)过点 作
作 于点
于点 ,则
,则
在 中,
中,
 ……(10分)
……(10分)
由(2)知四边形 是菱形,
是菱形,
∴
∴

【解析】略

练习册系列答案
相关题目

 (3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由。
(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由。 经过点(0,10)
经过点(0,10)
 中,已知二次函数
中,已知二次函数 的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3). (3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
(3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由