题目内容
如图,两个反比例函数y= 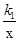 和y=
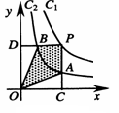
和y= 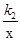 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
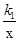 和y=
和y= 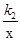 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
| A.k1+k2 | B.k1-k2 | C.k1·k2 | D.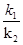 |
B
根据题意可得四边形PAOB的面积=S矩形OCPD-SOBD-SOAC,
由反比例函数y="k/x" 中k的几何意义,可知其面积为k1-k2.
故选B.
由反比例函数y="k/x" 中k的几何意义,可知其面积为k1-k2.
故选B.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
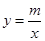 的图象和一次函数
的图象和一次函数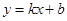 的图象的两个交点.
的图象的两个交点.
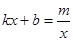 的解(请直接写出答案);
的解(请直接写出答案);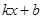 >
>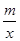 的解集(请直接写出答案).
的解集(请直接写出答案).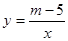 ,当
,当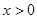 时,其图象位于第一象限,则m的取值范围是 ,此时
时,其图象位于第一象限,则m的取值范围是 ,此时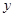 随
随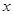 的增大而 。
的增大而 。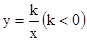 的图像上一点,过D作DE⊥x轴于E, DC⊥y轴于C,一次函数y=-x+m与y=-
的图像上一点,过D作DE⊥x轴于E, DC⊥y轴于C,一次函数y=-x+m与y=-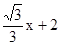 的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.
的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值. 的图像上有三点(
的图像上有三点( ,
, ),(
),( ,
, ),(
),( ,
,  )若
)若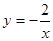 图象上有两点
图象上有两点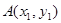 和
和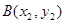 ,若
,若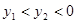 ,则
,则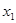 与
与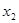 的关系是( )
的关系是( )



 , 且
, 且 ,它的图象经过A(-2,m)和B(1, n)两点.则m与n的大小关系是
,它的图象经过A(-2,m)和B(1, n)两点.则m与n的大小关系是 (
( ,x>0)的函数值
,x>0)的函数值 随
随 的增大而增大,则一次函数
的增大而增大,则一次函数 的图象大致是( )
的图象大致是( )
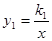 (其中k1>0)和
(其中k1>0)和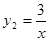 在第一象限内的图象依次是C1和 C2,点P在C1上。矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF垂直x轴于F点,且图中阴影部分面积为13,则EF﹕AC为( )
在第一象限内的图象依次是C1和 C2,点P在C1上。矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF垂直x轴于F点,且图中阴影部分面积为13,则EF﹕AC为( )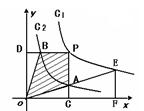
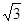 D.2﹕
D.2﹕