题目内容
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(-2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2014次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(-2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2014次相遇地点的坐标是( )| A、(-1,1) | B、(-2,0) | C、(-1,-1) | D、(1,-1) |
分析:利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
解答: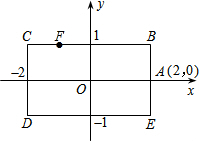 解:由题意可得:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
解:由题意可得:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×
=4,物体乙行的路程为12×
=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×
=8,物体乙行的路程为12×2×
=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×
=12,物体乙行的路程为12×3×
=24,在A点相遇;
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2014÷3=671…1,
故两个物体运动后的第2014次相遇地点的是:第一次相遇地点,
即物体甲行的路程为12×1×
=4,物体乙行的路程为12×1×
=8;
此时相遇点F的坐标为:(-1,1),
故选:A.
 解:由题意可得:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
解:由题意可得:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×
| 1 |
| 3 |
| 2 |
| 3 |
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×
| 1 |
| 3 |
| 2 |
| 3 |
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×
| 1 |
| 3 |
| 2 |
| 3 |
…
此时甲乙回到原出发点,则每相遇三次,两点回到出发点,
∵2014÷3=671…1,
故两个物体运动后的第2014次相遇地点的是:第一次相遇地点,
即物体甲行的路程为12×1×
| 1 |
| 3 |
| 2 |
| 3 |
此时相遇点F的坐标为:(-1,1),
故选:A.
点评:此题主要考查了行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2014次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2014次相遇地点的坐标是( )| A、(2,0) | B、(-1,1) | C、(-2,1) | D、(-1,-1) |
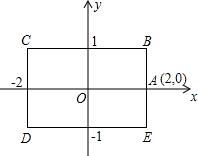 (2012•济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
(2012•济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( ) 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2013次相遇地点的坐标是