题目内容
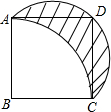 如图所示,ABCD是正方形,
如图所示,ABCD是正方形, 的圆心在B处,
的圆心在B处, 是以AC为直径的半圆.设AB=a,则阴影部分的面积是________.
是以AC为直径的半圆.设AB=a,则阴影部分的面积是________.
 a2
a2分析:连结AC,根据AB=a,得出正方形ABCD的面积,求出AC的值,求出S△ABC和S半圆ADC的值,再根据
 的圆心在B处,得出S扇形ABC的值,最后得出S弓形AmC=S扇形ABC-S△ABC,从而得出阴影部分的面积.
的圆心在B处,得出S扇形ABC的值,最后得出S弓形AmC=S扇形ABC-S△ABC,从而得出阴影部分的面积.解答:
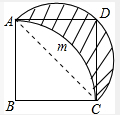 解:连结AC.
解:连结AC.∵AB=a,
∴正方形ABCD的面积是a2,
AC=
 =
= a,
a,S△ABC=
 a2,
a2,∴S半圆ADC=
 π(
π( )2=
)2= πa2,
πa2,∵
 的圆心在B处,
的圆心在B处,∴S扇形ABC=
 πa2,
πa2,∴S弓形AmC=S扇形ABC-S△ABC=
 πa2-
πa2- a2,
a2,∴阴影部分的面积=S半圆ADC-S弓形AmC=
 πa2-(
πa2-( πa2-
πa2- a2)=
a2)= a2.
a2.故答案为:
 a2.
a2.点评:此题考查了扇形面积的计算,用到的知识点是正方形、扇形、弓形、三角形的面积公式,解题的关键是作出辅助线,灵活运用有关公式求出阴影部分的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
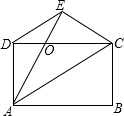 如图所示,ABCD是矩形,AB=4cm,AD=3cm.把矩形沿直线AC折叠,点B落在E处,连接DE.四边形ACED是什么图形?为什么?它的面积是多少?
如图所示,ABCD是矩形,AB=4cm,AD=3cm.把矩形沿直线AC折叠,点B落在E处,连接DE.四边形ACED是什么图形?为什么?它的面积是多少? 18、如图所示,ABCD是正方形,BE⊥BF,BE=BF,试判断AE与FC的位置关系,并给出证明.
18、如图所示,ABCD是正方形,BE⊥BF,BE=BF,试判断AE与FC的位置关系,并给出证明.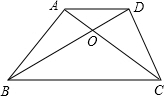 如图所示.ABCD是梯形,AD∥BC,AD<BC,AB=AC且AB⊥AC,BD=BC,AC,BD交于O.求∠BCD的度数.
如图所示.ABCD是梯形,AD∥BC,AD<BC,AB=AC且AB⊥AC,BD=BC,AC,BD交于O.求∠BCD的度数. (2013•泰州一模)一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为
(2013•泰州一模)一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为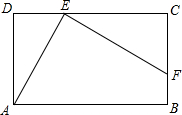 如图所示,ABCD是矩形,E在CD上,F在BC上,∠AEF=90°.
如图所示,ABCD是矩形,E在CD上,F在BC上,∠AEF=90°.