题目内容
关于x，y的方程组：
的解x，y满足：
，求k的取值范围．
解：∵2x+y=k-1，且2x+y≥3，
∴k-1≥3，
∴k≥4，
解关于x，y的方程组：，
解得：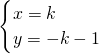
，
∴x-y=k-（-k-1）=2k+1≤17，
∴k≤8，
∴k的取值范围是：4≤k≤8．
分析：先求出方程组的解，可用k表示出x，y的值，再根据不等式组得出关于k的不等式，求出k的取值范围即可．
点评：此题主要考查了二元一次方程组的解法以及不等值的解法，根据已知用k表示出x，y得出关于k的不等式是解题关键．
∴k-1≥3，
∴k≥4，
解关于x，y的方程组：
，解得：
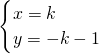，∴x-y=k-（-k-1）=2k+1≤17，
∴k≤8，
∴k的取值范围是：4≤k≤8．
分析：先求出方程组的解，可用k表示出x，y的值，再根据不等式组得出关于k的不等式，求出k的取值范围即可．
点评：此题主要考查了二元一次方程组的解法以及不等值的解法，根据已知用k表示出x，y得出关于k的不等式是解题关键．
练习册系列答案
培优三好生系列答案
相关题目
如图，直线y=x+m与双曲线y=关于x，y的方程组
的解是方程3x+2y=10的解，那么a的值为（ ）
|
| A、-2 | B、2 | C、-1 | D、1 |