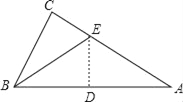
[题目]有一直角三角形纸片.∠C＝90°.BC＝6.AC＝8.现将△ABC按如图那样折叠.使点A与点B重合.折痕为DE.则CE的长为( )A. 2 B. C. D. 4 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】有一直角三角形纸片，∠C＝90°，BC＝6，AC＝8，现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则CE的长为（　　）

A. 2 B. C. D. 4

【答案】B

【解析】

已知，∠C=90°BC=6，AC=8，由勾股定理求AB，根据翻折不变性，可知△DAE≌△DBE，从而得到BD=AD，BE=AE，设CE=x，则AE=8-x，在Rt△CBE中，由勾股定理列方程求解．

∵△CBE≌△DBE，

∴BD=BC=6，DE=CE，

在RT△ACB中，AC=8，BC=6，

∴AB==10．

∴AD=AB-BD=10-6=4．

根据翻折不变性得△EDA≌△EDB

∴EA=EB

∴在Rt△BCE中，设CE=x，

则BE=AE=8-x，

∴BE2=BC2+CE2，

∴（8-x）2=62+x2，

解得x=．

故选B．

练习册系列答案

(1)直接写出点C，D的坐标：C ，D ；

(2)四边形ABCD的面积为；

(3)点P为线段BC上一动点(不含端点)，连接PD，PO.求证：∠CDP+∠BOP=∠OPD.

【题目】如图，在Rt△ABC中，∠ACB＝90°，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB.

(1)求证：∠1＝∠2.

(2)过点M作AB的垂线交CD的延长线于点E，连结AE，BE.求证：CM＝EM.

【题目】大华服装厂生产一件秋冬季外套需面料1.2米，里料0.8米，已知面料的单价比里料的单价的2倍还多10元，一件外套的布料成本为76元．
（1）求面料和里料的单价；
（2）该款外套9月份投放市场的批发价为150元/件，出现购销两旺态势，10月份进入批发淡季，厂方决定采取打折促销．已知生产一件外套需人工等固定费用14元，为确保每件外套的利润不低于30元．
①设10月份厂方的打折数为m，求m的最小值；（利润=销售价﹣布料成本﹣固定费用）
②进入11月份以后，销售情况出现好转，厂方决定对VIP客户在10月份最低折扣价的基础上实施更大的优惠，对普通客户在10月份最低折扣价的基础上实施价格上浮．已知对VIP客户的降价率和对普通客户的提价率相等，结果一个VIP客户用9120元批发外套的件数和一个普通客户用10080元批发外套的件数相同，求VIP客户享受的降价率．

【题目】某营业厅对手机话费业务有如下的优惠：
优惠规则：
①用户手机账户原有话费不能低于240元；
②办理业务时，首先从手机账户中一次性扣除240元，并把这240元抵为300元话费，然后将这300元话费分12次，在每月的15号等额返还到手机账户；
③每月1号从手机账户中扣除话费49元，当月不再扣除其他任何费用；
④每月1号手机账户的话费余额不足以扣除49元时，视为欠费，则当月不再返还等额的话费．
小明的手机账户中原有话费400元，办理了这项优惠业务，设小明的手机账户中每个月末的话费余额是y（元），月数为x（个），则
（1）每个月等额返还的话费是元，第2个月末的话费余额是元；
（2）求y关于x的函数关系式；
（3）若不续费，小明的手机第几个月会欠费？

【题目】某调查小组采用简单随机抽样方法，对某市部分中小学生一天中阳光体育运动时间进行了抽样调查，并把所得数据整理后绘制成如下的统计图：

（1）该调查小组抽取的样本容量是多少？
（2）求样本学生中阳光体育运动时间为1.5小时的人数，并补全占频数分布直方图；
（3）请估计该市中小学生一天中阳光体育运动的平均时间．