题目内容
 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P沿路线0→C→B运动.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P沿路线0→C→B运动.(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)求△COB的面积.
(3)当△POB的面积是△COB的面积的一半时,求出这时点P的坐标.
分析:(1)由图可知,点C是交点,求两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;根据图象可判断出y1>y2时,x的取值范围;
(2)令y2=0,根据函数关系式可得出x的值,结合(1)中点C的横坐标,根据三角形面积公式,求出即可;
(3)由题意可知,当点P的纵坐标是点纵坐标的一半时,△POB的面积是△COB的面积的一半,把y值分别代入y1=x和y2=-2x+6,求出x的值,即可求出点P的坐标.
(2)令y2=0,根据函数关系式可得出x的值,结合(1)中点C的横坐标,根据三角形面积公式,求出即可;
(3)由题意可知,当点P的纵坐标是点纵坐标的一半时,△POB的面积是△COB的面积的一半,把y值分别代入y1=x和y2=-2x+6,求出x的值,即可求出点P的坐标.
解答:解:(1)由题意,列方程组
,
解得
,
∴点C的坐标为(2,2),
∴当x>2时,y1>y2;
(2)令y2=0,则-2x+6=0,
解得,x=3,
∴S△COB=
×3×2=3;
(3)∵△POB的面积是△COB的面积的一半,
∴点P的纵坐标y=1,
把y=1分别代入y1=x和y2=-2x+6,
得,x1=1,x2=
,
∴点P的坐标为(1,1)或(
,1).
|
解得
|
∴点C的坐标为(2,2),
∴当x>2时,y1>y2;
(2)令y2=0,则-2x+6=0,
解得,x=3,
∴S△COB=
| 1 |
| 2 |
(3)∵△POB的面积是△COB的面积的一半,
∴点P的纵坐标y=1,
把y=1分别代入y1=x和y2=-2x+6,
得,x1=1,x2=
| 5 |
| 2 |
∴点P的坐标为(1,1)或(
| 5 |
| 2 |
点评:本题主要考查了一次函数图象及交点、动点问题等,体现了数形结合思想.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
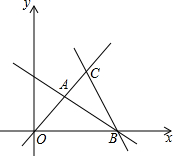 交于点A.
交于点A.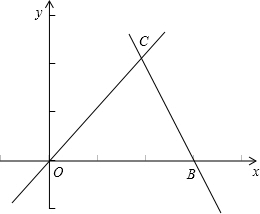 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.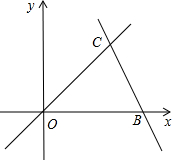 如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.
如图,直线OC、BC的函数关系式分别为y=x和y=-2x+6,动点P(x,0)在OB上移动(0<x<3),过点P作直线l与x轴垂直.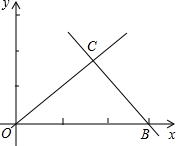 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直. 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6.