题目内容
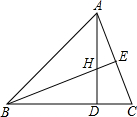 已知:如图,在△ABC中,AD⊥BC,垂足为D,AD与BE相交于点H,且BH=AC,DH=DC.
已知:如图,在△ABC中,AD⊥BC,垂足为D,AD与BE相交于点H,且BH=AC,DH=DC.
(1)求∠ABC的度数,
(2)BE与AC有怎样的位置关系,请说明理由.
解:(1)∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
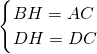 ,
,
∴Rt△BDE≌Rt△ADC(HL),
∴AD=BD,
∴∠BAD=∠ABD,
∵∠ADB=90°,
∴∠ABC= ×(180°-90°)=45°.
×(180°-90°)=45°.
(2)BE⊥AC,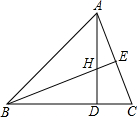
理由是:∵Rt△BDE≌Rt△ADC,
∴∠CAD=∠HBD,
∵∠ADB=90°,
∴∠HBD+∠BHD=90°,
∵∠BHD=∠AHE,
∴∠AHE+∠CAD=90°,
∴∠AEH=180°-90°=90°,
∴BE⊥AC.
分析:(1)求出∠BDE=∠ADC=90°,根据HL证Rt△BDE≌Rt△ADC,推出AD=BD,推出∠BAD=∠ABD即可.
(2)根据Rt△BDE≌Rt△ADC得出∠CAD=∠HBD,求出∠HBD+∠BHD=90°,即可求出∠AHE+∠CAD=90°,根据三角形内角和定理求出∠AEH=90°,即可得出答案.
点评:本题考查了等腰三角形的判定和性质,三角形的内角和定理,垂直定义,全等三角形的性质和判定的应用,注意:直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.全等三角形的对应边相等,对应角相等.
∴∠BDE=∠ADC=90°,
在Rt△BDE和Rt△ADC中,
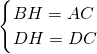 ,
,∴Rt△BDE≌Rt△ADC(HL),
∴AD=BD,
∴∠BAD=∠ABD,
∵∠ADB=90°,
∴∠ABC=
 ×(180°-90°)=45°.
×(180°-90°)=45°.(2)BE⊥AC,

理由是:∵Rt△BDE≌Rt△ADC,
∴∠CAD=∠HBD,
∵∠ADB=90°,
∴∠HBD+∠BHD=90°,
∵∠BHD=∠AHE,
∴∠AHE+∠CAD=90°,
∴∠AEH=180°-90°=90°,
∴BE⊥AC.
分析:(1)求出∠BDE=∠ADC=90°,根据HL证Rt△BDE≌Rt△ADC,推出AD=BD,推出∠BAD=∠ABD即可.
(2)根据Rt△BDE≌Rt△ADC得出∠CAD=∠HBD,求出∠HBD+∠BHD=90°,即可求出∠AHE+∠CAD=90°,根据三角形内角和定理求出∠AEH=90°,即可得出答案.
点评:本题考查了等腰三角形的判定和性质,三角形的内角和定理,垂直定义,全等三角形的性质和判定的应用,注意:直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,