题目内容
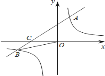
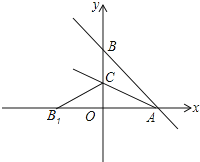
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 轴上一点,沿直线
轴上一点,沿直线![]() 折叠
折叠![]() 刚好落在
刚好落在![]() 轴上
轴上![]() 处.
处.
请解答下列问题:
(1)![]() ,
,![]() 两点的坐标分别为_____________,____________.
两点的坐标分别为_____________,____________.
(2)求![]() 的长;
的长;
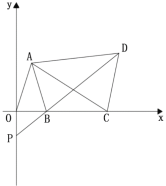
(3)在![]() 轴上存在点
轴上存在点![]() ,使三角形
,使三角形![]() 为等腰三角形,直接写出
为等腰三角形,直接写出![]() 的坐标_____________.
的坐标_____________.
【答案】(1)A(3,0),B(0,4);(2)1.5;(3)(3-![]() ,0)或(3+
,0)或(3+![]() ,0)或(
,0)或(![]() ,0)或(-3,0).
,0)或(-3,0).
【解析】
(1)对于直线解析式,分别令x与y为0,求出y与x的值,即可确定出A与B的坐标;
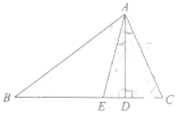
(2)在直角三角形AOB中,利用勾股定理求出AB的长,设OC为x,则B1C=BC=4-x,计算即可解答;
(3)在直角三角形AOC中,利用勾股定理求出AC的长,如图所示,分三种情况考虑:当AP=AC;当AP′=AC;当P″A=P″C,作AC的垂直平分线交OA于点P″,分别求出P的坐标即可.
(1)对于直线y=-![]() x+4,
x+4,

令x=0,得到y=4;令y=0,得到x=3,
则A(3,0),B(0,4);
(2)在Rt△ABC中,OA=3,OB=4,
根据勾股定理得:AB=![]() =5,
=5,
∴OB1=AB-OA=2,
设OC为x,则B1C=BC=4-x,
![]() ,
,
解得:x=1.5.
(3)在Rt△OAC中,OA=3,OC=1.5,
根据勾股定理得:AC=![]() ,
,
如图所示,要使△PAC为等腰三角形,分三种情况考虑:
当AP=AC时,P坐标为(3-![]() ,0);
,0);
当AP′=AC时,P′坐标为(3+![]() ,0);
,0);
当P″A=P″C时,作AC的垂直平分线交OA于点P″,
设OP″=x,根据勾股定理得:x2+1.52=(3-x)2,
解得:x=![]() ,即P″(
,即P″(![]() ,0),
,0),
当PC=AC时, P″′坐标为(-3,0);
综上,点P的坐标为(3-![]() ,0)或(3+
,0)或(3+![]() ,0)或(
,0)或(![]() ,0)或(-3,0).
,0)或(-3,0).

 阅读快车系列答案
阅读快车系列答案