Question

如图：两个等腰直角三角形的两个直角顶点A、C都在y=

k

x

上，若D（-8，0），则k=

 

．

Answer 1

分析：分别过A、C作x轴的垂线，设垂足为E、F；首先设出点E的坐标，由于等腰直角三角形的斜边等于斜边上高的2倍，可得EF=4，进而可表示出点F的坐标，即可表示出点A、C的坐标，然后将它们代入双曲线解析式中，通过联立方程组求得k的值．

解答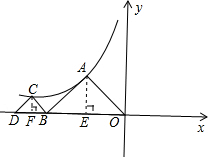：解：过A、C作AE⊥x轴于E，CF⊥x轴于F；
设A（-x，x），则C（-x-4，4-x）；
代入双曲线的解析式中得：

x= k -x 4-x= k -x-4

，
消去k，得：-x²=x²-16，解得x²=8；
∴k=-x•x=-x²=-8．
故答案为：-8．

点评：此题主要考查的是反比例函数解析式的确定，还涉及到等腰直角三角形的性质，难度适中．