题目内容
如图，以等腰△ABC的腰AB为直径画半圆O，交AC于E，交BC于D．（1）求证：D是BC的中点；
（2）若∠BAC=50°，求
 | DE |
分析：（1）首先连接AD，由以等腰△ABC的腰AB为直径画半圆O，根据三线合一的性质，可证得D是BC的中点；
（2）首先连接OD，OE，由圆周角定理，可求得∠BOD的度数，由等腰三角形的性质，可求得∠AOE的度数，继而求得答案．
（2）首先连接OD，OE，由圆周角定理，可求得∠BOD的度数，由等腰三角形的性质，可求得∠AOE的度数，继而求得答案．
解答：
（1）证明：连接AD，
∵AB为直径，
∴∠ADB=90°，
即AD⊥BC，
∵AB=AC，
∴BD=CD，
即D是BC的中点；
（2）解：连接OD，OE，
∵∠BAC=50°，AB=AC，AD⊥BC，
∴∠BAD=25°，
∴∠BOD=2∠BAD=50°，
∵OA=OE，
∴∠OEA=∠BAC=50°，
∴∠AOE=180°-∠BAC-∠OEA=80°，
∴∠DOE=180°-∠BOD-∠AOE=50°，
∴
的度数为50°．
（1）证明：连接AD，∵AB为直径，
∴∠ADB=90°，
即AD⊥BC，
∵AB=AC，
∴BD=CD，
即D是BC的中点；
（2）解：连接OD，OE，
∵∠BAC=50°，AB=AC，AD⊥BC，
∴∠BAD=25°，
∴∠BOD=2∠BAD=50°，
∵OA=OE，
∴∠OEA=∠BAC=50°，
∴∠AOE=180°-∠BAC-∠OEA=80°，
∴∠DOE=180°-∠BOD-∠AOE=50°，
∴
|
| DE |
点评：此题考查了圆周角定理与等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
24、如图，以等腰△ABC的腰AB为⊙O的直径交底边BC于D，DE⊥AC于E．
如图，以等腰△ABC中的腰AB为直径作⊙O，交底边BC于点D．过点D作DE⊥AC，垂足为E．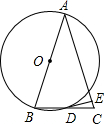
结论是否成立？请说明理由；
（2012•孝感模拟）如图，以等腰△ABC的一腰AB上的点O为圆心，以OB为半径作圆，⊙O交底边BC于点D．过D作⊙O的切线DE，交AC于点E．