题目内容
牧童在河边A处放牛，家在河边B处，时近傍晚，牧童驱赶牛群先到河边饮水，然
后在天黑前赶回家，已知A点到河边C的距离为500米，点B到河边的距离为700米，且CD=500米．
（1）请在原图上画出牧童回家的最短路线；
（2）求出最短路线的长度．
解：（1）作A关于直线CD的对称点A′，连接A′B交CD于P点，
即为所求作的点．
（2）由作图可得最短路程为A′B的距离，过A′作A′F⊥BD的延长线于F，
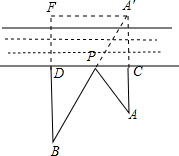
则DF=A'C=AC=500m，A′F=CD=500m，BF=700+500=1200m，
根据勾股定理可得，A′B=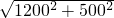
=1300米．
分析：（1）作A关于直线CD的对称点A′，连接A′B交CD于P点，即为所求作的点；
（2）最短路程即是A‘B的距离，过A′作A′F⊥BD的延长线于F，根据勾股定理求得即可．
点评：此题考查了线路最短的问题，确定动点为何位置是关键综合运用勾股定理的知识．
即为所求作的点．
（2）由作图可得最短路程为A′B的距离，过A′作A′F⊥BD的延长线于F，
则DF=A'C=AC=500m，A′F=CD=500m，BF=700+500=1200m，
根据勾股定理可得，A′B=
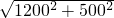=1300米．分析：（1）作A关于直线CD的对称点A′，连接A′B交CD于P点，即为所求作的点；
（2）最短路程即是A‘B的距离，过A′作A′F⊥BD的延长线于F，根据勾股定理求得即可．
点评：此题考查了线路最短的问题，确定动点为何位置是关键综合运用勾股定理的知识．
练习册系列答案
相关题目
后在天黑前赶回家，已知A点到河边C的距离为500米，点B到河边的距离为700米，且CD=500米．
