题目内容
已知一次函数y=2x+1,则它的图象与坐标轴围成的三角形面积是
.
| 1 |
| 4 |
| 1 |
| 4 |
分析:求得函数与坐标轴的交点,然后根据三角形的面积公式即可求得三角形的面积.
解答:解:∵一次函数的关系式是y=2x+1,
∴当x=0时,y=1;当y=0时,x=-
,
∴它的图象与坐标轴围成的三角形面积是:
×1×|-
|=
.
故答案是:
.
∴当x=0时,y=1;当y=0时,x=-
| 1 |
| 2 |
∴它的图象与坐标轴围成的三角形面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案是:
| 1 |
| 4 |
点评:本题主要考查了一次函数图象上点的坐标特征.求线段的长的问题一般是转化为求点的坐标的问题解决.

练习册系列答案
相关题目
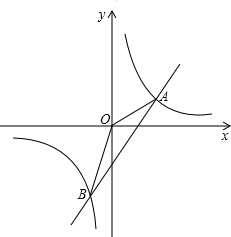 已知一次函数y=2x-k与反比例函数
已知一次函数y=2x-k与反比例函数