题目内容
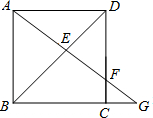如图，已知点F是正方形ABCD的边CD上的点，
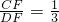，AF与BD相交于点E，AF的延长线交BC的延长线于点G．
求AE：EG的值．
解：∵四边形ABCD是正方形，
∴AD∥BG，AD=BC，
∵AD∥BG，，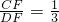
∴
，
∴
，
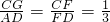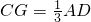∵AD=BC，
∴
，
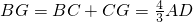∵AD∥BG，
∴
．
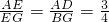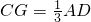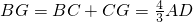分析：根据正方形的性质和平行线分线段成比例的性质可得AD=BC，，依此可得，再根据平行线分线段成比例的性质可得AE：EG的值．
点评：考查了正方形的性质和平行线分线段成比例的性质，解题的关键是得到．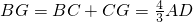
∴AD∥BG，AD=BC，
∵AD∥BG，
，∴
，∴
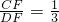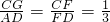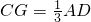，∵AD=BC，
∴
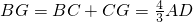，∵AD∥BG，
∴
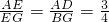．分析：根据正方形的性质和平行线分线段成比例的性质可得AD=BC，
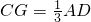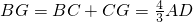，依此可得，再根据平行线分线段成比例的性质可得AE：EG的值．点评：考查了正方形的性质和平行线分线段成比例的性质，解题的关键是得到
． 
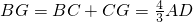练习册系列答案
相关题目
，
如图，已知正方形ABCD的边长为4，将正方形置于平面直角坐标系xOy中，使AB在x轴的负半轴上，A点的坐标是（-1，0）．
如图，已知B（0，4），点A在第一象限，且AB⊥y轴，∠A=30°．
如图，已知点A、B、C是数轴上三点，O为原点．点C对应的数为6，BC=4．AB=12．
CQ，设运动时间为t（t＞0）．