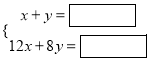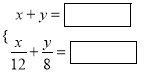Question

【题目】已知一次函数的图像与轴、轴分别相交于点、，点在该函数的图像上， 到轴、轴的距离分别为、．

（）当为线段端点时，求的值．

（）直接写出的范围，并求当时点的坐标．

（）若在线段上存在无数个点，使（为常数），求的值．

Answer 1

【答案】（1）2；（2）， 或；（3）3．

【解析】试题分析：（1）对于一次函数解析式，求出A的坐标，即可求出P为A时d1+d2的值；

（2）根据题意确定出d1+d2的范围，设P（m，3m-6），表示出d1+d2，分类讨论m的范围，根据d1+d2=3求出m的值，即可确定出P的坐标；

（3）设P（m，3m-6），表示出d1与d2，由P在线段上求出m的范围，利用绝对值的代数意义表示出d1与d2，代入d1+ad2=6，根据存在无数个点P求出a的值即可.

试题解析：（）由题意得，当为时，则， ，

∴；

（）设，则，

当时， ，

当时， ，

∴，

当时， ，

∴，

综上， ，当时，若，则， ，∴；

当时，若，则， ，

∴；

（）设P（m，2m-4），∴d1=|3m-6|，d2=|m|，

∵P在线段AB上，

∴0≤m≤2，

∴d1=6-3m，d2=m，

∵d1+ad2=6，

∴6-3m+am=6，即（a-3）m=0，

∵有无数个点，

∴a=3．