题目内容
已知抛物线 与x轴有两个不同的交点.
与x轴有两个不同的交点.
(1)求抛物线的对称轴;
(2)求c的取值范围;
(3)若此抛物线与x轴两交点之间的距离为2,求c的值.
解:(1)∵a= ,b=1,
,b=1,
∴对称轴为直线x=- =-1,
=-1,
(2)∵抛物线 与x轴有两个不同的交点,
与x轴有两个不同的交点,
∴△>0,∴c< ;
;
(3)∵对称轴为直线x=-1,抛物线与x轴两交点之间的距离为2,
∴抛物线与x轴两交点为(0,0)和(-2,0),
把(0,0)的坐标代入 ,得c=0.
,得c=0.
分析:(1)根据a,b的值,直接利用抛物线对称轴公式求出即可;
(2)利用抛物线 与x轴有两个不同的交点,得出△>0,进而求出即可;
与x轴有两个不同的交点,得出△>0,进而求出即可;
(3)根据抛物线与x轴两交点之间的距离为2,对称轴为直线x=-1得出交点坐标即可,进而求出c的值.
点评:此题主要考查了二次函数的性质,熟练利用数形结合得出图象上点的坐标是解题关键.
 ,b=1,
,b=1,∴对称轴为直线x=-
 =-1,
=-1,(2)∵抛物线
 与x轴有两个不同的交点,
与x轴有两个不同的交点,∴△>0,∴c<
 ;
;(3)∵对称轴为直线x=-1,抛物线与x轴两交点之间的距离为2,
∴抛物线与x轴两交点为(0,0)和(-2,0),
把(0,0)的坐标代入
 ,得c=0.
,得c=0.分析:(1)根据a,b的值,直接利用抛物线对称轴公式求出即可;
(2)利用抛物线
 与x轴有两个不同的交点,得出△>0,进而求出即可;
与x轴有两个不同的交点,得出△>0,进而求出即可;(3)根据抛物线与x轴两交点之间的距离为2,对称轴为直线x=-1得出交点坐标即可,进而求出c的值.
点评:此题主要考查了二次函数的性质,熟练利用数形结合得出图象上点的坐标是解题关键.

练习册系列答案
相关题目
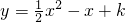 与x轴有两个交点.
与x轴有两个交点.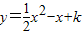 与x轴有两个交点.
与x轴有两个交点. 与x轴有两个交点,则m的取值范围是
与x轴有两个交点,则m的取值范围是
 与x轴有两个交点,则m的取值范围是
与x轴有两个交点,则m的取值范围是  与x轴有两个交点,则m的取值范围是
.
与x轴有两个交点,则m的取值范围是
.