Question

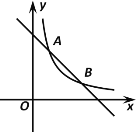
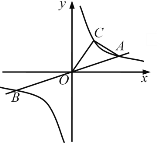
【题目】如图，在平面直角坐标系中，正比例函数y＝x的图像与反比例函数y＝的图像交于A，B两点，且点A的坐标为（6，a）．

（1）求反比例函数的表达式；

（2）已知点C（b，4）在反比例函数y＝的图像上，点P在x轴上，若△AOC的面积等于△AOP的面积的两倍，请求出点P的坐标．

Answer 1

【答案】（1）反比例函数的表达式为y＝；（2）点P的坐标为（，0）或（－，0）．

【解析】

（1）先求解A的坐标，再用待定系数法求反比例函数解析式，

（2）先求解C的坐标，利用S△AOC＝S四边形COEA－S△OAE＝S四边形COEA－S△COD＝S梯形CDEA求解，再求，利用面积公式可得答案．

解：（1）∵点A（6，a）在正比例函数y＝x的图像上

∴a＝×6＝2

∵点A（6，2）在反比例函数y＝的图像上

∴2＝，

k＝12

∴反比例函数的表达式为y＝．

（2）分别过点C，A作CD⊥轴，AE⊥轴，垂足分别为点D，E．

∵点C（b，4）在反比例函数y＝的图像上

∴4＝，b＝3，即点C的坐标为（3，4）

∵点A，C都在反比例函数y＝的图像上

∴S△OAE＝S△COD＝×12＝6

∴S△AOC＝S四边形COEA－S△OAE＝S四边形COEA－S△COD＝S梯形CDEA

∴S△AOC＝×(CD＋AE)·DE＝×(4＋2)×(6－3)＝9

∵△AOC的面积等于△AOP的面积的两倍

∴S△AOP＝S△AOC＝，

设点P的坐标为（m，0）

则S△AOP＝×2·︱m︱＝，．

∴m＝，

∴点P的坐标为（，0）或（－，0）．