题目内容
图象的顶点为（-2，-2），且经过原点的二次函数的关系式是
- A.y=
（x+2）2-2 - B.y=（x-2）2-2
- C.y=2（x+2）2-2
- D.y=2（x-2）2-2
A
分析：由抛物线的顶点坐标为（-2，-2），设顶点式：y=a（x+2）2-2，把原点（0，0）代入求a即可．
解答：∵图象的顶点为（-2，-2），
∴设顶点式：y=a（x+2）2-2，
把原点（0，0）代入，得0=a（0+2）2-2，
解得a=，
∴抛物线解析式为y=（x+2）2-2．
故选A．
点评：本题考查了抛物线的顶点坐标与抛物线解析式的关系，抛物线的顶点式：y=a（x-h）2+k，顶点坐标为（h，k）．
分析：由抛物线的顶点坐标为（-2，-2），设顶点式：y=a（x+2）2-2，把原点（0，0）代入求a即可．
解答：∵图象的顶点为（-2，-2），
∴设顶点式：y=a（x+2）2-2，
把原点（0，0）代入，得0=a（0+2）2-2，
解得a=
，∴抛物线解析式为y=
（x+2）2-2．故选A．
点评：本题考查了抛物线的顶点坐标与抛物线解析式的关系，抛物线的顶点式：y=a（x-h）2+k，顶点坐标为（h，k）．
练习册系列答案
相关题目
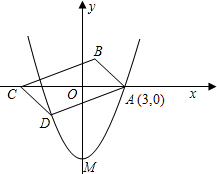为（-5，0），四边形ABCD是以AC为对角线的平行四边形．
（2013•呼和浩特）如图，已知二次函数的图象经过点A（6，0）、B（-2，0）和点C（0，-8）．
如图，已知二次函数y=（x-1）2的图象的顶点为C点，图象与直线y=x+m的图象交于A、B两点，其中A点的坐标为（3，4），B点在y轴上．