题目内容
在?ABCD中，∠A，∠B的度数之比为5：4，则∠C等于
- A.60°
- B.80°
- C.100°
- D.120°
C
分析：根据平行四边形的性质可知∠A，∠B互补，根据已知可以求出∠A，∠B的度数，而∠C是∠A的对角，所以相等．
解答：在?ABCD中，
∵AD∥BC，
∴∠A+∠B=180°，
∠A，∠B的度数之比为5：4，
∴∠A=100°，∠B=80°，
∴∠C=∠A=100°
故选C．
点评：此题主要考查平行四边形的性质：（1）邻角互补；（2）平行四边形的两组对角分别相等．
分析：根据平行四边形的性质可知∠A，∠B互补，根据已知可以求出∠A，∠B的度数，而∠C是∠A的对角，所以相等．
解答：在?ABCD中，
∵AD∥BC，
∴∠A+∠B=180°，
∠A，∠B的度数之比为5：4，
∴∠A=100°，∠B=80°，
∴∠C=∠A=100°
故选C．
点评：此题主要考查平行四边形的性质：（1）邻角互补；（2）平行四边形的两组对角分别相等．
练习册系列答案
相关题目
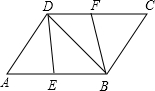如图，在?ABCD中，E、F分别为边AB、CD的中点，连接DE、BF、BD．
如图，在?ABCD中，EF∥AB，MN∥BC，MN与EF交于点O，且O点在对角线上，图中面积相等的四边形有（ ）
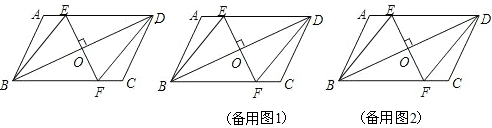
如图，在?ABCD中，点E在边BC上，点F在BC的延长线上，且BE=CF．