题目内容
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC, BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F, DF="6."
(1) 求AE的长;
(2) 求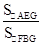 的值.
的值.
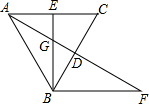
(1) 求AE的长;
(2) 求
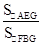 的值.
的值.
(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)根据等边三角形的性质和判定推出∠C=60°,求出∠CBF=60°,∠F=30°,解直角三角形求出BD,即可得出答案.
(2)求出BF长,根据相似三角形的性质和判定得出即可.
试题解析:(1)∵在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,
∴AC=AB=BC.∴△ABC是等边三角形.∴∠C=60°.
∵BF∥AC,∴∠CBF=∠C=60°.
∵AD⊥BC,∴∠FDB=90°.∴∠F=30°.
∵DF=6,∴BD=
 .
.∵AE=EC=BD=DC,∴AE=
 .
.(2)∵∠BDF=90°,∠F=30°,BD=
 ,∴BF=2DB=
,∴BF=2DB= .
.∵AC∥BF,∴△AEG∽△FBG.
∴
 .
.
练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目

 S△ABC;
S△ABC; .
.

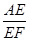 =3,求
=3,求 的值.
的值.
 =a,
=a, =b(a>0,b>0)则
=b(a>0,b>0)则 的值为( )
的值为( )
