题目内容
如图,点A是反比例函数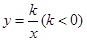
 上一点,作AB⊥x轴于点B,且△AOB的面积为2,点A坐标为(-1,m)。
上一点,作AB⊥x轴于点B,且△AOB的面积为2,点A坐标为(-1,m)。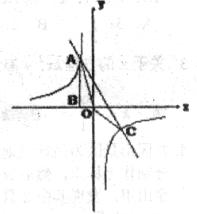
(1)求k和m的值。
(2)若直线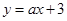 经过点A,交另一支双曲线于点C,求△AOC的面积。
经过点A,交另一支双曲线于点C,求△AOC的面积。
(3)指出x取何值时,一次函数的值大于反比例函数的值,直接写出结果。
(4)在y轴上是否存在点P,使得△PAC的面积为6,如果存在,请求出点P的坐标;若不存在,请说明理由.
(1)-4,4(2) (3)
(3) (4)存在,
(4)存在,
解析试题分析:(1)根据△AOB的面积求出A点的坐标,然后根据A点坐标确定出反比例函数的解析式即可.
(2)将△AOC分成△AOM和COM两部分进行求解.先根据直线AC的解析式经过点A求出a的值,再求出M的坐标,即可得出OM的长,然后根据A、C的纵坐标即可求出△AOC的面积;
(3)由图象,根据A、C的横坐标即可得出答案.
(4)假设存在,设P(0,c),由 即可求解.
即可求解.
试题解析:解:(1)

(2)把 代入
代入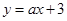 中
中
得
由




∴C(4,-1) A(-1,4)
设直线与y轴交于点D,易得D(6,3)

(3)
(4)设




又
∴
∴

考点:反比例函数与一次函数的交点问题

练习册系列答案
相关题目
 与
与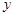 的值相等,则已知程方组
的值相等,则已知程方组 中
中 的值是( ).
的值是( ).
| A.1 | B. | C. | D. |
若一组数据1,3,4,5,x中,有唯一的众数是1,这组数据的中位数是( )
| A.1 | B.2 | C.3 | D.4 |
(本题满分8分)九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是
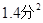 ,则成绩较为整齐的是 队.
,则成绩较为整齐的是 队. 将函数 的图象向右平移
的图象向右平移 个单位得到的新图象的函数解析式为( )。
个单位得到的新图象的函数解析式为( )。
A. | B. |
C. | D. |
 的图象经过点A(?3,?2).
的图象经过点A(?3,?2).