题目内容
如图,点O、A、B的坐标分别为(0,0)、(3,0)、(3,-2),将△O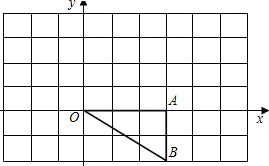 AB绕点O按逆时针方向旋转90°得到△OA′B′.
AB绕点O按逆时针方向旋转90°得到△OA′B′.(1)画出旋转后的△OA′B′,并求点B′的坐标;
(2)求在旋转过程中,点A所经过的路径
 | AA′ |
分析:(1)按要求画即可,其中旋转90度是关键.
(2)根据弧长公式计算即可.
(2)根据弧长公式计算即可.
解答: 解:(1)如图△OA′B′为所示,点B′的坐标为(2,3);(4分)
解:(1)如图△OA′B′为所示,点B′的坐标为(2,3);(4分)
(2)△OAB绕点O逆时针旋转90°后得△OA′B′,
点A所经过的路径
是圆心角为90°,半径为3的扇形OAA′的弧长,
所以l=
×(2π×3)=
π.(7分)
即点A所经过的路径
的长度为
π.(8分)
 解:(1)如图△OA′B′为所示,点B′的坐标为(2,3);(4分)
解:(1)如图△OA′B′为所示,点B′的坐标为(2,3);(4分)(2)△OAB绕点O逆时针旋转90°后得△OA′B′,
点A所经过的路径
 |
| AA′ |
所以l=
| 1 |
| 4 |
| 3 |
| 2 |
即点A所经过的路径
 |
| AA′ |
| 3 |
| 2 |
点评:本题的难点是第二题,做第二题时要分清圆心角的度数和半径的长,即可利用弧长公式计算.

练习册系列答案
相关题目
 6、如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为( )
6、如图,点A,B,C的坐标分别为(2,4),(5,2),(3,-1).若以点A,B,C,D为顶点的四边形既是轴对称图形,又是中心对称图形,则点D的坐标为( ) 29、如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,要推理得出△ABE≌△ACD,可以补充的一个条件是
29、如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,要推理得出△ABE≌△ACD,可以补充的一个条件是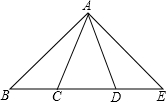 如图,点C、D在△ABE的边BE上,且AB=AE,AC=AD,求证:BC=DE.
如图,点C、D在△ABE的边BE上,且AB=AE,AC=AD,求证:BC=DE.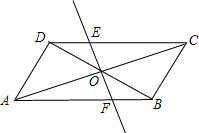 于点E、F.
于点E、F. 如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,
如图,点P为等边△ABC的边AB上一点,Q为BC延长线上一点,AP=CQ,PQ交AC于D,