Question

已知实数a，b，c满足abc=-1，a+b+c=4，，则a²+b²+c²=________．

Answer 1

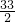
分析：把a²-3a-1变形后，将abc=-1，a+b+c=4代入得到结果为a（b-1）（c-1），同理将已知等式的第二、三个分母变形，将已知等式左边通分并利用同分母分式的加法法则计算，整理后将abc=-1，a+b+c=4代入求出ab+ac+bc的值，将所求的式子利用公式（a+b+c）²=a²+b²+c²+2ab+2ac+2bc变形后，将a+b+c及ab+ac+bc的值代入即可求出值．
解答：∵abc=-1，a+b+c=4，
∴a²-3a-1=a²-3a+abc=a（bc+a-3）=a（bc-b-c+1）=a（b-1）（c-1），
∴=，
同理可得：=，=，
又++=，
∴++=，
∴=，即（a-1）（b-1）（c-1）=（a-1）+（b-1）+（c-1），
整理得：（abc-ab-ac-bc+a+b+c-1）=a+b+c-3，
将abc=-1，a+b+c=4代入得：ab+bc+ac=-，
则a²+b²+c²=（a+b+c）²-2（ab+bc+ac）=．
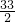故答案为：．
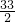点评：此题考查了分式的混合运算，利用了整体代入的数学思想，其技巧性较强，其中把已知等式的各分母进行适当的变形是解本题的关键．