题目内容
已知直线y=-
x+
交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为______.
| ||
| 3 |
| 3 |
∵直线y=-
x+
交x轴于点A,交y轴于点C,
∴A(3,0),B(0,
),
∵OC=
,OA=3,
∴tan∠CAO=
=
,
∴∠CAO=30°,
当点B在x轴上,且BC=AB时(如图1),
∵OC⊥x轴,
∴点O是AB的中点,
∵点A(3,0),
∴B(-3,0);
当BC=AB时(如图2),设B(a,0),则a2+(
)2=(3-a)2,解得a=1,
∴B(1,0);
当点B在y轴上时(如图3):
∵∠CAO=30°,∠AOC=90°,
∴∠ACO=60°,
∴∠BCA=180°-∠ACO=180°-60°=120°,
若BC=AC,则∠BAC=
=
=30°,
∴此种情况符合题意,
设点B(0,y),则(y-
)2=32+(
)2,解得y=3
,
∴B(0,3
).
综上所述,符合条件的B点坐标为:(-3,0);(0,3
);(1,0).
故答案为:(-3,0);(0,3
);(1,0).

| ||
| 3 |
| 3 |
∴A(3,0),B(0,
| 3 |
∵OC=
| 3 |
∴tan∠CAO=
| OC |
| OA |
| ||
| 3 |
∴∠CAO=30°,
当点B在x轴上,且BC=AB时(如图1),
∵OC⊥x轴,

∴点O是AB的中点,
∵点A(3,0),
∴B(-3,0);
当BC=AB时(如图2),设B(a,0),则a2+(
| 3 |
∴B(1,0);
当点B在y轴上时(如图3):
∵∠CAO=30°,∠AOC=90°,

∴∠ACO=60°,
∴∠BCA=180°-∠ACO=180°-60°=120°,
若BC=AC,则∠BAC=
| 180°-∠ABC |
| 2 |
| 180°-120° |
| 2 |
∴此种情况符合题意,
设点B(0,y),则(y-
| 3 |
| 3 |
| 3 |
∴B(0,3
| 3 |
综上所述,符合条件的B点坐标为:(-3,0);(0,3
| 3 |
故答案为:(-3,0);(0,3
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.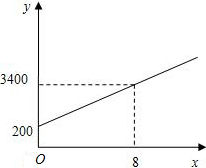 元.又知“为民”出租车公司有小、中、大三种型号货车供出租,本次派出的货车每种型号货车不少于3台,各种型号货车载重量和预计运费如下表所示.
元.又知“为民”出租车公司有小、中、大三种型号货车供出租,本次派出的货车每种型号货车不少于3台,各种型号货车载重量和预计运费如下表所示. 度是每分钟3个单位长度,直线PM交BC于点Q,当直线PM与正方形OABC没有公共点的时候,动点P就停止运动.
度是每分钟3个单位长度,直线PM交BC于点Q,当直线PM与正方形OABC没有公共点的时候,动点P就停止运动. 当两车油箱中剩余油量相同时,那么两车的行驶路程相差多少千米?
当两车油箱中剩余油量相同时,那么两车的行驶路程相差多少千米?
 格不变,而制版费900元按六折收费,且甲乙两厂都规定一次印刷数量至少是500份.
格不变,而制版费900元按六折收费,且甲乙两厂都规定一次印刷数量至少是500份.