题目内容
 19、如图,已知△ABC是等边三角形,D,E分别在边BC,AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,BE和CF
19、如图,已知△ABC是等边三角形,D,E分别在边BC,AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,BE和CF(1)请找出图中全等三角形,用符号“≌”表示;
(2)判断四边形ABDF是怎样的四边形,并说明理由.
分析:(1)根据等边三角形的性质定理,即可找到全等的三角形;
(2)根据等边三角形的性质,即可求出∠ABD=∠FDC=∠DCE=60°,∠EAF=∠AFE=∠AEF=60°推出AB∥FD,AF∥BC,然后依据平行四边形的判定,即可判定四边形ABDF是平行四边形.
(2)根据等边三角形的性质,即可求出∠ABD=∠FDC=∠DCE=60°,∠EAF=∠AFE=∠AEF=60°推出AB∥FD,AF∥BC,然后依据平行四边形的判定,即可判定四边形ABDF是平行四边形.
解答:解:(1)△ABE≌△CAF,△BEC≌△FCD,△EFC≌△EDB;
(2)四边形ABDF是平行四边形,
证明:∵△ABC是等边三角形,且CD=CE,
∴∠ABD=∠FDC=∠DCE=60°AB=BC,
∴AB∥FD,
∵EF=AE,
∴∠EAF=∠AFE=∠AEF=60°,
∵AF∥BC,
∴四边形ABDF是平行四边形.
(2)四边形ABDF是平行四边形,
证明:∵△ABC是等边三角形,且CD=CE,
∴∠ABD=∠FDC=∠DCE=60°AB=BC,
∴AB∥FD,
∵EF=AE,
∴∠EAF=∠AFE=∠AEF=60°,
∵AF∥BC,
∴四边形ABDF是平行四边形.
点评:本题主要考查等边三角形的性质和全等三角形的判定及性质,解题的关键在于找到全等三角形,结合相关的性质定理求出相等的角.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.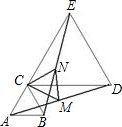 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.