题目内容
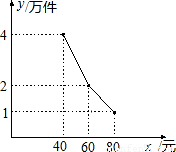
当前大学生就业形势严峻,大学生小涛自主研发了某产品,决定自主创业,经过市场调研,开办工厂需投资90万元,每件产品生产成本需40元,每月还需支付其它开支15万元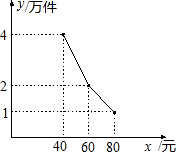 ,预计该产品每月销售y(万件)与销售单价x(元)之间的函数关系如下图所示.
,预计该产品每月销售y(万件)与销售单价x(元)之间的函数关系如下图所示.
(1)求预计每月销售量y(万件)与销售单价x(元)之间的函数关系;
(2)小涛开办工厂,估计最快需几个月可以收回投资;
(3)小涛希望在收回投资后,每月盈利25万元,则工厂每月销售多少件产品?
解:(1)设预计每月销售量y(万件)与销售单价x(元)之间的函数关系式为:y=kx+b,由题意得:
①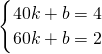 (40≤x≤60),
(40≤x≤60),
解得: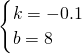 ,
,
∴y=-0.1x+8,
②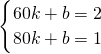 (60≤x≤80),
(60≤x≤80),
解得: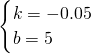 ,
,
∴y=-0.05x+5,
(2)设每月利润为W万元,则有
当40≤x≤60时,W=(-0.1x+8)(x-40)-15=-0.1(x-60)2+25,
当60≤x≤80时,W=(-0.05x+5)(x-40)-15=-0.05(x-70)2+30,
即:当40≤x≤60时,x=60时,W的最大值为25万元,
当60≤x≤80时,x=70时,W的最大值为30万元.
所以最快需3个月可以收回90万元的投资.
(3)当收回投资后,每月要盈利25万元,
即:当售价定为60元,
25万=20000×(60-40)-15万,
即生产2万件,
当售价定为80元,
25万=10000×(60-40)-15万,
即生产1万件.
分析:(1)利用图象上点的坐标利用待定系数法代入y=kx+b,求出一次函数解析式即可;
(2)利用图象上的点的坐标得出售价与利润之间的关系,进而求出答案;
(3)结合(2)中结论可以得出定价与销量之间的关系即可得出答案.
点评:此题主要考查了一次函数的应用以及待定系数法求一次函数解析式等知识,表示出产品的利润结合函数关系式分析是解决问题的关键.
①
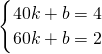 (40≤x≤60),
(40≤x≤60),解得:
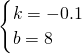 ,
,∴y=-0.1x+8,
②
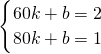 (60≤x≤80),
(60≤x≤80),解得:
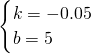 ,
,∴y=-0.05x+5,
(2)设每月利润为W万元,则有
当40≤x≤60时,W=(-0.1x+8)(x-40)-15=-0.1(x-60)2+25,
当60≤x≤80时,W=(-0.05x+5)(x-40)-15=-0.05(x-70)2+30,
即:当40≤x≤60时,x=60时,W的最大值为25万元,
当60≤x≤80时,x=70时,W的最大值为30万元.
所以最快需3个月可以收回90万元的投资.
(3)当收回投资后,每月要盈利25万元,
即:当售价定为60元,
25万=20000×(60-40)-15万,
即生产2万件,
当售价定为80元,
25万=10000×(60-40)-15万,
即生产1万件.
分析:(1)利用图象上点的坐标利用待定系数法代入y=kx+b,求出一次函数解析式即可;
(2)利用图象上的点的坐标得出售价与利润之间的关系,进而求出答案;
(3)结合(2)中结论可以得出定价与销量之间的关系即可得出答案.
点评:此题主要考查了一次函数的应用以及待定系数法求一次函数解析式等知识,表示出产品的利润结合函数关系式分析是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
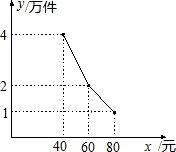 ,预计该产品每月销售y(万件)与销售单价x(元)之间的函数关系如下图所示.
,预计该产品每月销售y(万件)与销售单价x(元)之间的函数关系如下图所示.