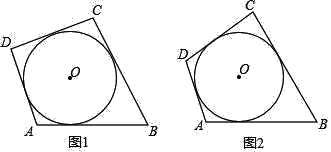题目内容
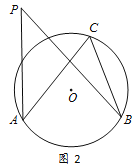
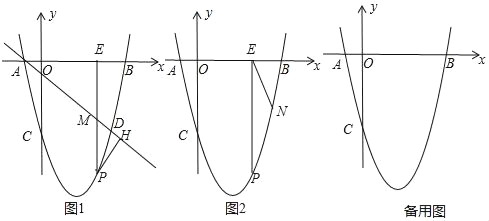
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
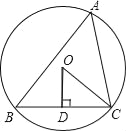
(3)在(2)的条件下,如图2,在直线EP的右侧、x轴下方的抛物线上是否存在点N,过点N作NG⊥x轴交x轴于点G,使得以点E、N、G为顶点的三角形与△AOC相似?如果存在,请直接写出点G的坐标:如果不存在,请说明理由.
【答案】(1)y=x2﹣3x﹣4(2)4+4![]() (3)存在
(3)存在
【解析】
(1)先由锐角三角函数的定义求得C的坐标,从而得到点B的坐标,设抛物线的解析式为y=a(x+1)(x-4),将点C的坐标代入求解即可;
(2)先求得抛物线的对称轴,从而得到点D(3,-4),然后可求得直线AD的解析式y=-x-1,故∠BAD=45°,接下来证明△PMD为等腰直角三角形,所当PM有最大值时三角形的周长最大,设P(a,a2-3a-4),M(-a-1),则PM=-a2+2a+3,然后利用配方可求得PM的最大值,最后根据△MPH的周长=(1+![]() )PM求解即可;
)PM求解即可;
(3)设点G的坐标为(a,0),则N(a,a2﹣3a﹣4), 若![]() =
=![]() 时,△AOC∽△EGN,
时,△AOC∽△EGN,
则![]() =
=![]() ,求出a 的值,若
,求出a 的值,若![]() =
=![]() 时,△AOC∽△NGE,则
时,△AOC∽△NGE,则![]() =4,
=4,
求出a的值,舍去不符合的即可得出答案.
(1)∵点A的坐标为(﹣1,0),
∴OA=1.
又∵tan∠OAC=4,
∴OC=4,
∴C(0,﹣4).
∵OC=OB,
∴OB=4,
∴B(4,0).
设抛物线的解析式为y=a(x+1)(x﹣4)
∵将x=0,y=﹣4代入得:﹣4a=﹣4,解得a=1,
∴抛物线的解析式为y=x2﹣3x﹣4.
(2)∵抛物线的对称轴为x=﹣![]() =
=![]() ,C(0,﹣4),
,C(0,﹣4),
∵点D和点C关于抛物线的对称轴对称,
∴D(3,﹣4)
设直线AD的解析式为y=kx+b.
∵将A(﹣1,0)、D(3,﹣4)代入得:![]() ,
,
解得k=﹣1,b=﹣1,
∴直线AD的解析式y=﹣x﹣1.
∵直线AD的一次项系数k=﹣1,
∴∠BAD=45°.
∵PM平行于y轴,
∴∠AEP=90°,
∴∠PMH=∠AME=45°.
∴△MPH的周长=PM+MH+PH=PM+![]() MP+
MP+![]() PM=(1+
PM=(1+![]() )PM.
)PM.
设P(a,a2﹣3a﹣4),则M(a,﹣a﹣1),
则PM═﹣a﹣1﹣(a2﹣3a﹣4)=﹣a2+2a+3=﹣(a﹣1)2+4.
∴当a=1时,PM有最大值,最大值为4.
∴△MPH的周长的最大值=4×(1+![]() )=4+4
)=4+4![]() ;
;
(3)存在
点G的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
附解题过程:设点G的坐标为(a,0),则N(a,a2﹣3a﹣4)
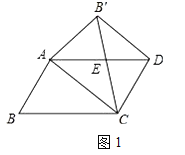
①如图1,
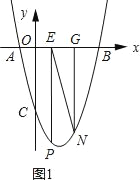
若![]() =
=![]() 时,△AOC∽△EGN.
时,△AOC∽△EGN.
则![]() =
=![]() ,整理得:a2+a﹣8=0.
,整理得:a2+a﹣8=0.
得:a=![]() (负值舍去)∴点G为(
(负值舍去)∴点G为(![]() ,0)
,0)
②如图2,
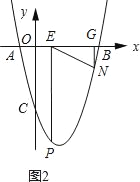
若![]() =
=![]() 时,△AOC∽△NGE.
时,△AOC∽△NGE.
则![]() =4,整理得:4a2﹣11a﹣17=0.
=4,整理得:4a2﹣11a﹣17=0.
得:a=![]() (负值舍去)
(负值舍去)
∴点G为(![]() ,0).
,0).
综上所述,点G的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).

【题目】某商贸公司有![]() 、
、![]() 两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(立方米/件) | 质量(吨/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 两种型号,体积一共是20立方米,质量一共是10.5吨,求
两种型号,体积一共是20立方米,质量一共是10.5吨,求![]() 、
、![]() 两种型号商品各有几件?
两种型号商品各有几件?
(2)物资公司现有可供使用的货车每辆额定载重3.5吨,容积为6立方米,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

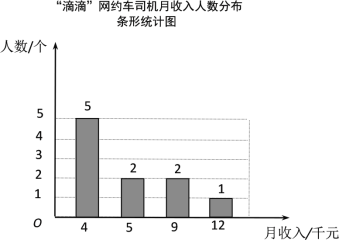
根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.