Question

【题目】在矩形中，是的中点，以点为直角顶点的直角三角形的两边、始终与矩形、两边相交，，，

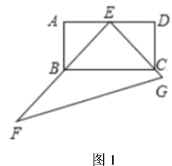
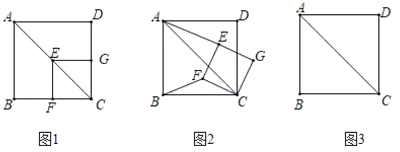
（1）如图1，当、分别过点、时，求的大小；

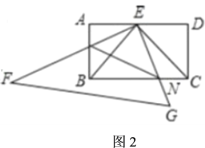
（2）在（1）的条件下，如图2，将绕点按顺时针方向旋转，当旋转到与重合时停止转动．若、分别与、相交于点、．

①在旋转过程中，四边形的面积是否发生变化？若不变，求四边形的面积；若要变，请说明理由．

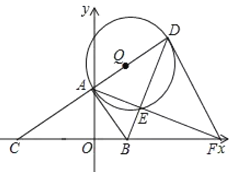
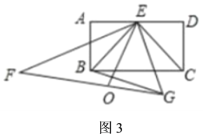
②如图3，设点为的中点，连结、，若，当的长度最小时，求的值．

Answer 1

【答案】（1）45°；（2）①不变，4；② ．

【解析】

（1）证明△AEB≌△DEC（SAS），可得EB=EC，根据等腰直角三角形的性质即可解决问题．
（2）①四边形BMEN的面积不变．证明△MEB≌△NEC（ASA），推出S△MEB=S△ENC，可得S四边形EMBN=S△EBC．
②如图当E，B，O共线时，OB的值最小，作GH⊥OE于H．想办法求出BH，GH即可解决问题．

解：（1）如图1中，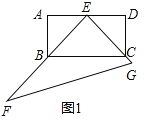

∵四边形ABCD是矩形，
∴AB=DC，∠A=∠D=90°，
∵AE=DE，
∴△AEB≌△DEC（SAS），
∴EB=EC，
∵∠BEC=90°，
∴∠EBC=45°．
（2）①结论：四边形BMEN的面积不变．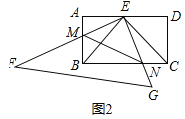

理由：由（1）可知：∠EBM=∠ECN=45°，
∵∠MEN=∠BEC=90°，
∴∠BEM=∠CEN，
∵EB=EC，
∴△MEB≌△NEC（ASA），
∴S△MEB=S△ENC，
∴S四边形EMBN=S△EBC=×4×2=4．
②如图当E，B，O共线时，OB的值最小，作GH⊥OE于H．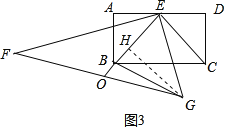

∵OF=OG，∠FEG=90°，
∴OE=OF=OG=4，
∵∠F=30°，
∴∠EGF=60°，
∴△EOG是等边三角形，∵GH⊥OE，
∴GH=2，OH=EH=2，
∵BE=2，
∴OB=4-2，
∴BH=2-（4-2）=2-2，
∴tan∠EBG= ．