题目内容
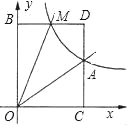
【题目】如图,已知正比例函数y=ax与反比例函数y=![]() 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)求上述两函数的表达式;
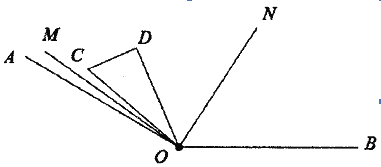
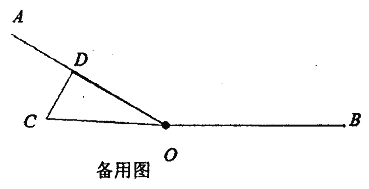
(2)M(m,n)是反比例函数图象上的一个动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A点作直线AC∥y轴交x轴于点C,交直线MB于点D.若s四边形OADM=6,求点M的坐标,并判断线段BM与DM的大小关系,说明理由;
(3)探索:x轴上是否存在点P.使△OAP是等腰三角形?若存在,求出点P的坐标; 若不存在,说明理由.
【答案】(1)反比例函数的表达式为:y=![]() ,正比例函数的表达式为y=
,正比例函数的表达式为y=![]() x;(2)BM=DM;(3)存在,(
x;(2)BM=DM;(3)存在,(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(6,0)或(
,0)或(6,0)或(![]() ,0)
,0)
【解析】
(1)将A(3,2)分别代入y=![]() ,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
(2)由S△OMB=S△OAC=![]() |k|=3,可得S矩形OBDC=12;即OCOB=12;进而可得mn的值,故可得BM与DM的大小;比较可得其大小关系;
|k|=3,可得S矩形OBDC=12;即OCOB=12;进而可得mn的值,故可得BM与DM的大小;比较可得其大小关系;
(3)存在.由(2)可知D(3,4),根据矩形的性质得A(3,2),分为OA为等腰三角形的腰,OA为等腰三角形的底,分别求P点坐标.
解:(1)将A(3,2)分别代入y=![]() ,y=ax中,得:2=
,y=ax中,得:2=![]() ,3a=2
,3a=2
∴k=6,a=![]() ,
,
∴反比例函数的表达式为:y=![]() ,
,
正比例函数的表达式为y=![]() x;
x;
(2)BM=DM
理由:∵S△OMB=S△OAC=![]() ×|k|=3
×|k|=3
∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12
即OCOB=12
∵OC=3
∴OB=4
即n=4
∴m=![]() =
=![]() ,即点M的坐标为(
,即点M的坐标为(![]() ,4)
,4)
∴MB=![]() ,MD=3﹣
,MD=3﹣![]() =
=![]() ,
,
∴MB=MD;
(3)存在.
由(2)得A(3,2),OA=![]()
当OA为等腰三角形的腰时,P(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(6,0),
,0)或(6,0),
当OA为等腰三角形的底,P(![]() ,0).
,0).
∴满足条件的P点坐标为(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(6,0)或(
,0)或(6,0)或(![]() ,0).
,0).

 名校课堂系列答案
名校课堂系列答案