题目内容
下列计算中正确的是（ ）
| A、（p-q）2=p2-q2 |
| B、（a+2b）2=a2+4ab+b2 |
| C、（a2+1）2=a4+2a+1 |
| D、（-s-t）2=s2+2st+t2 |
考点：完全平方公式
专题：
分析：根据完全平方公式对各选项分析判断利用排除法求解．
解答：解：A、应为（p-q）2=p2-2pq+q2，故本选项错误；
B、应为（a+2b）2=a2+4ab+4b2，故本选项错误；
C、应为（a2+1）2=a4+2a2+1，故本选项错误；
D、（-s-t）2=s2+2st+t2，故本选项正确．
故选D．
B、应为（a+2b）2=a2+4ab+4b2，故本选项错误；
C、应为（a2+1）2=a4+2a2+1，故本选项错误；
D、（-s-t）2=s2+2st+t2，故本选项正确．
故选D．
点评：本题主要考查完全平方公式的变形，熟记公式结构是解题的关键．完全平方公式：（a±b）2=a2±2ab+b2．
练习册系列答案
相关题目
下列命题中不正确的是（ ）
| A、等腰直角三角形都相似 |
| B、顶角相等的等腰三角形一定相似 |
| C、全等形是相似形 |
| D、不相似的图形可能是全等形 |
有理数a、b在数轴上的位置如图，则a+b的值为（ ）| A、大于0 | B、小于0 |
| C、等于0 | D、无法确定 |
下列各式计算正确的是（ ）
| A、a2+a3=a5 |
| B、a6÷a2=a3 |
| C、a2•a3=a6 |
| D、（x2）3=x6 |
若|x+3|+
=0，则x+y的值为（ ）
| y-2 |
| A、1 | B、-1 | C、5 | D、-5 |
如图，在菱形ABCD中，不一定成立的是（ ）| A、四边形ABCD是平行四边形 |
| B、AC⊥BD |
| C、△ABD是等边三角形 |
| D、∠CAD=∠CAB |
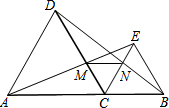如图，点C为线段AB上一动点（不与点A，B重合），在AB同侧分别作等边△ACD和等边△CBE，连结AE与BD，AE与CD交于点M，CE与BD交于点N，连结MN，则对于结论①AE=DB；②EM=BN；③△CMN是等边三角形；④MN∥AB，其中正确结论的个数是（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
已知直角梯形的一腰长为6cm，这腰与底所成的角为30°，那么另一腰长是（ ）
| A、3cm | B、1.5cm |
| C、6cm | D、9cm |