题目内容
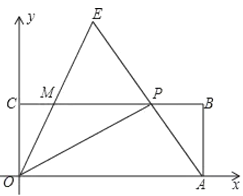
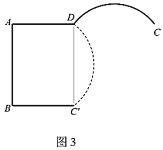
【题目】已知，二次函数y＝ax2+2ax﹣3a（a＞0）图象的顶点为C，与x轴交于A，B两点（点A在点B的左侧），点C，B关于过点A的直线l对称，直线l与y轴交于D．
（1）求A，B两点坐标及直线l的解析式；
（2）求二次函数解析式；
（3）在第三象限抛物线上有一个动点E，连接OE交直线l于点F，求
的最大值．
【答案】（1）点A、B的坐标分别为：（﹣3，0）、（1，0），直线l的表达式为：y＝﹣
x﹣
；（2）y＝
；（3）
．
【解析】
（1）对于y＝ax2＋2ax3a，令y＝0，则x＝3或1，求出点A、B的坐标，利用点C，B关于直线l对称得AC＝AB＝4，求出a的值，进而求解；
（2）由（1）得到a的值，故可求解；
（3）利用△HEF∽△DOF，得到
＝
＝﹣
x2﹣
x+，即可求解．
（1）对于y＝ax2+2ax﹣3a，令y＝0，则x＝﹣3或1，
则点A、B的坐标分别为：（﹣3，0）、（1，0），
则函数的对称轴为：x＝﹣1，则顶点C坐标为：（﹣1，﹣4a），
∵点C，B关于直线l对称，如下图：
∴AC＝AB＝4，
即（﹣3+1）2+（0+4a）2＝42，
解得：a＝
（负值已舍去），
故点C的坐标为：（﹣1，﹣2），
则BC＝
＝4＝AB＝AC，
故△ABC为等边三角形，
∵点C，B关于直线l对称，
则BC∠⊥AD，故∠BAD＝30°，
∵tan30°=
则设直线l的表达式为：y＝﹣x+b，
将点A的坐标代入得0=﹣×3+b
并解得：b＝﹣，
故直线l的表达式为：y＝﹣x﹣；
（2）由（1）知a＝，
故抛物线的表达式为：y＝x2+x﹣
；
（3）∵直线l的表达式为：y＝﹣x﹣；
∴点D的坐标为：（0，﹣），即OD＝，
过点E作y轴的平行线交AD于点H，
设点E（x，x2+x﹣），则点H（x，﹣x﹣），
则EH＝（﹣x﹣）﹣（x2+x﹣）＝﹣x2﹣
x+，
∵HE∥y轴，
∴△HEF∽△DOF，
∴＝＝﹣x2﹣x+=-（x+）2+，
∵
0，故
有最大值，
当x＝﹣时，最大值为．
