题目内容
在直角坐标系中,函数y=
的图象与直线x+y=3相交于点A、B,则点A与点B到原点的距离分别是( )
| 2 |
| x |
| A、5,5 | ||||
B、
| ||||
C、5,
| ||||
D、
|
分析:首先联立y=
和y=-x+3,求出x、y的值,然后求出点A与点B到原点的距离.
| 2 |
| x |
解答:解:∵函数y=
的图象与直线x+y=3相交于点A、B,
∴
,
解得
或
,
∴点A坐标为(1,2),点B坐标为(2,1),
∴点A与点B到原点的距离分别
,
.
故选D.
| 2 |
| x |
∴
|
解得
|
|
∴点A坐标为(1,2),点B坐标为(2,1),
∴点A与点B到原点的距离分别
| 5 |
| 5 |
故选D.
点评:本题主要考查反比例函数与一次函数的交点问题的知识,解答本题的关键求出A、B两点的坐标,本题难度一般.

练习册系列答案
相关题目
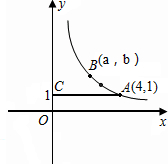 曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.
曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.