Question

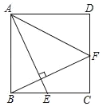
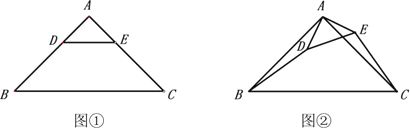
【题目】如图①，在等腰直角三角形中，，，D，E分别在上，且，此时有，．

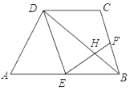
(1)如图①中 绕点A旋转至如图②时上述结论是否仍然成立？若成立，请证明；若不成立，请说明理由.

(2)将图①中的绕点A旋转至DE与直线AC垂直，直线BD交CE于点F，若，，请画出图形，并求出BF的长.

Answer 1

【答案】(1)仍然成立；(2)画图见解析；长为或.

【解析】

（1）结论：BD＝CE，BD⊥CE．如图1中，延长BD交CE的延长线于H．证明△BAD≌△CAE（SAS），即可解决问题；（2）分两种中情况分别求解①当逆时针旋转角度是45°时，②当逆时针旋转角度是225°时，先证明△ABD≌△ACE（SAS），从而求解DE，EC 的边长，再通过角的代换证明BF⊥EC，再证明Rt△DEF∽Rt△CEG，通过对应边成比例，求出FC的长度，最后再直角三角形△BCF用勾股定理求得BF的长度．

解：(1) 仍然成立

延长交于点，

和都是等腰直角三角形，

，，

，

，

，

，

， ，

；

(2)如图，长为或，

∵DE与直线AC垂直，

①当逆时针旋转角度是45°时，如图2：

在△ABD和△ACE中，

AE＝AD，∠BAD＝∠CAE＝45°，AB＝AC，

∴△ABD≌△ACE（SAS）

∴BD＝EC，

∵AB＝20，AD＝5，

∴AC＝20，AE＝5，

∵∠DAE＝90°，

∴DE＝10，

∵△AED是等腰直角三角形，

∴AG＝GE＝5，

∴GC＝15，

在直角三角形GEC中，EC＝5，

又∵∠ABD＝∠ACE，∠BCA＝45°，∠ABC＝45°，

∴∠DBC+∠BCA+∠ACE＝90°，

∴BF⊥EC，

∵∠EFD＝∠EGC＝90°，∠EDF＝∠ECG，

∴Rt△DEF∽Rt△CEG，

∴ ，

∴，

∴EF＝，

∴FC＝4，

在Rt△ABC中，BC＝20，

在Rt△BCF中，BF＝；

②当逆时针旋转角度是225°时，如图3，

在△ABD和△ACE中，

AE＝AD，BAD＝∠CAE＝45°，AB＝AC，

∴△ABD≌△ACE（SAS）

∴BD＝EC，

∵AB＝20，AD＝5，

∴AC＝20，AE＝5，

∵∠DAE＝90°，

∴DE＝10，

∵△AED是等腰直角三角形，

∴AG＝GE＝5，

∴GC＝25，

在直角三角形GEC中，EC＝5，

又∵∠ABD＝∠ACE，∠ABC＝45°，∠ACB＝45°，

∴∠DBA+∠ABC+∠ACE＝90°，

∴BF⊥EC，

∵∠EFD＝∠EGC＝90°，∠EDF＝∠ECG，

∴Rt△DEF∽Rt△CEG，

∴，

∴，

∴EF＝，

∴FC＝，

在Rt△ABC中，BC＝20，

在Rt△BCF中，BF＝；