题目内容
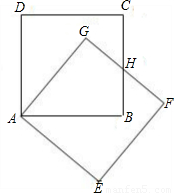
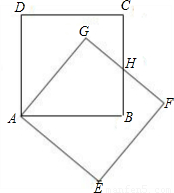
 把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).
把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).(1)试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
(2)若正方形的边长为2cm,重叠部分(四边形ABHG)的面积为
4
| ||
| 3 |
分析:(1)由正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,根据旋转的性质得到AG=AB,∠G=∠B=90°,于是Rt△AGH≌Rt△ABH,得到HG=HB;
(2)由于Rt△AGH≌Rt△ABH,则S四边形ABHG=2S△ABH=
,得到S△ABH=
,利用三角形的面积公式可求出BH=
,再录三角函数可得到∠2=30°,得到∠GAE,最后通过互余求出旋转角∠DAG.
(2)由于Rt△AGH≌Rt△ABH,则S四边形ABHG=2S△ABH=
4
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
解答: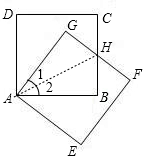 解:(1)线段HG与线段HB相等.理由如下:
解:(1)线段HG与线段HB相等.理由如下:
连AH,如图,
∵正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,
∴AD=AG,AB=AE,
∴AG=AB,∠G=∠B=90°,
在Rt△AGH和Rt△ABH中
,
∴Rt△AGH≌Rt△ABH(HL),
∴HG=HB;
(2)由(1)得,S四边形ABHG=2S△ABH=
(cm2),
∴S△ABH=
(cm2),
∴
•AB•BH=
,
而AB=2cm,
∴BH=
cm,
∴tan∠2=
=
,
∴∠2=30°,
∴∠GAB=60°,
∴∠DAG=90°-60°=30°,
即旋转的角度为30°.
 解:(1)线段HG与线段HB相等.理由如下:
解:(1)线段HG与线段HB相等.理由如下:连AH,如图,
∵正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,
∴AD=AG,AB=AE,
∴AG=AB,∠G=∠B=90°,
在Rt△AGH和Rt△ABH中
|
∴Rt△AGH≌Rt△ABH(HL),
∴HG=HB;
(2)由(1)得,S四边形ABHG=2S△ABH=
4
| ||
| 3 |
∴S△ABH=
2
| ||
| 3 |
∴
| 1 |
| 2 |
2
| ||
| 3 |
而AB=2cm,
∴BH=
2
| ||
| 3 |
∴tan∠2=
| ||||
| 2 |
| ||
| 3 |
∴∠2=30°,
∴∠GAB=60°,
∴∠DAG=90°-60°=30°,
即旋转的角度为30°.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形的性质、三角形全等的判定与性质以及特殊角的三角函数值.

练习册系列答案
相关题目
 24、把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
24、把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.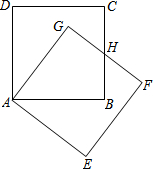 如图所示,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.
如图所示,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.